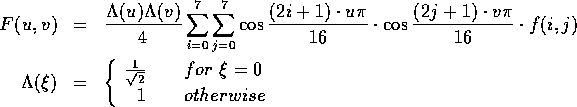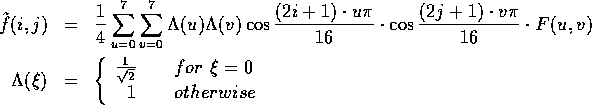CSA302
Lecture 7 - Compression Techniques
References:
Steinmetz, R., and Nahrstedt, K. (1995). Multimedia:
Computing, Communications & Applications. Prentice Hall. Chapter 6.
Aravind, R., et. al., (1993). Image
and Video Coding Standards.
JPEG/JBIG Home page
The Motivation for Compression
Multimedia data in general requires enormous amounts of storage and
bandwidth capacity. Continuous data, especially in the form of real-time
communications (e.g., audio/video-conferencing) would be impossible, given
the current nature of the Internet, and the real-time transmission of video
data would put enormous strain even on high-speed fiber optic networks.
In order to make feasible and cost-effective use of real-time communications over a data
network, or to store high volume data on digital media, data is usually
compressed to a fraction of the space/bandwidth requirements of its
uncompressed form.
Compression Techniques
There are a large number of proprietary and public-domain compression
techniques. We will look at some of the underlying features common to many
compressions techniques. We will then discuss JPEG (for still images), H.261 (for
video-conferencing), and MPEG (for video and audio).
Compression Requirements
Uncompressed multimedia data has extremely high data storage and bandwidth
requirements. Secondary storage requirements will be in the range of
gigabytes at least, buffer storage will be in the range of megabytes.
Bandwidth would need to support data transfer rates of up to 140Mbits per
second for a single user. Compression techniques would aim to
reduce the storage requirements to megabytes, and buffer storage and
bandwidth to kilobytes.
Compression in multimedia systems is subject to certain constraints: The
quality of the decompressed data should be as good as possible. Ideally,
compression and decompression should be hardware-independent (not only for
portability, but also to reduce cost). Finally, the processing of the
algorithm should not exceed certain time spans (e.g., de/compression of
video-conferencing data should be real-time, but sometimes it is acceptable
to spend large amounts of time compressing the source, as long as
decompression is fast, e.g., for retrieval of images).
This basic difference between the way information is consumed (by humans)
leads to a distinction between dialog mode applications and
retrieval mode applications.
In dialog mode application, where humans are interacting with each other
via multimedia information, the constraints on the codec
(compressor/decompressor, or coder/decoder) are imposed by human perception
characteristics. In order to maintain the impression of
face-to-face dialog the end-to-end delay should
not exceed 150 milliseconds, where a maximum of 50 milliseconds is the
delay introduced by the compression and decompression of the data, and 100
milliseconds is the maximum delay allowed by the transmission of the data
over a network, the communication protocol processing at the end system,
and the data transfer between the respective i/o devices.
In retrieval mode application, we must be able to perform fast forward and
backward retrieval, and simultaneous display of multimedia data. This
implies a fast search and retrieval of data from multimedia databases. It
should be possible to perform rapid and random access to single video
and audio frames in less than 0.5 seconds, which supports the perception
of interactivity. Decompression of images, video and audio should not be
dependent on other data units, to allow random access and editing.
Requirements which apply to both dialog and retrieval mode are that the
compression techniques should be parameterized, to support user-dependent
network and processing constraints (e.g., network connection speed and
processor speed), and the compression technique should not prevent the
decompressed data from being resized (in the case of images and video). It
must also be possible to synchronize video with audio, and with other media.
Basic Compression Techniques
Basic compression techniques fall into three broad categories:
source, entropy, and hybrid. Source compression is
lossy, which means that data is lost through the compression process.
However, entropy compression is lossless, which means that no data is lost
during compression. Most multimedia systems use hybrid techniques, which
are a combination of the two.
Entropy compression is media-independent - it does not take the media's
characteristics into account, but simply treats the data at a bit or byte
stream. Huffman coding is an example of an entropy compression technique.
On the other hand, source compression is dependent on the characteristics
of the specific media being compressed. Examples are Fast Fourier
Transform and Discrete Cosine Transform. Prior to compression, the
data may be converted from its original domain, (e.g., time), if it does not support high
compression factors, to a domain which does (e.g., frequency).
During this transformation, data is lost and is not recoverable, making the
relation between the uncompressed and compressed data streams one-way and lossy.
A Set of Typical Processing Steps

Preparation includes Analog-to-Digital conversion and generating an
approximate representation of the information. In the case of an image, it
is divided into blocks of 8x8 pixels, each pixels represented by a fixed
number of bits.
Processing is the first step of the compression process. If the
domain within which the data is to be compressed needs to be changed, it
can be done at this time. In the case of motion video, a transformation
from the time to the frequency domain may be performed to construct a
motion vector for each 8x8 block in consecutive frames.
Quantization specifies the granularity of the mapping of real numbers
into integers. There is consequently a reduction of space requirements, at the expense of
precision.
Entropy compression is usually the last step. The digital stream
resulting from quantization will be compressed without loss. For example,
Run-length compression replaces a sequence of identical numbers with the
number followed by a special symbol which doesn't occur in the stream
followed by the number of occurrences. E.g., 10000001 would be compressed
to 10!61.
The processing and quantization steps may be performed iteratively several
times in feedback loops. After compression, a data stream is built which
specifies, amongst other things, the compression technique used and any
error correction codes.
Decompression is the inverse of compression. Decompression
techniques can differ from the compression techniques in various ways. For
example, if the applications are symmetric, e.g., dialog applications,
then the coding and decoding should incur more or less the same costs, as
the importance here is the speed factor, rather than quality. However, if
data will be encoded once, but decoded many times, as is the case with an
image or video retrieval system, then whereas the decoding speed must
approximate real-time, the encoding time may be asymmetric to the decoding
time. Usually, better quality/compression ratios are obtained if encoding
time is not a factor.
Other Simple Compression Techniques
Vector Quantization
A data stream is divided into blocks of n bytes, where n >
1, A predefined table contains a set of patterns. For each block, the
most similar pattern in the table is identified, and the data stream is
gradually replaced with a sequence of pointers to the appropriate pattern
index. The decoder, which requires the same table of patterns, generates an
approximation to the original data stream. Pattern substitution is also
used in text compression. The major difference here is that the decoded
data stream must be identical to the original - an approximation may be
unintelligible!
Diatomic encoding
This is a variation of run-length coding based on a combination of two
data bytes. For a given media type the most common co-occurring pairs of
data bytes are identified. These are then replaced in the data stream by
single bytes that do not occur anywhere else in the stream.
Huffman coding
Different characters do not have to be coded with the same number of bits
(e.g., Morse code). Huffman coding analyses the data stream to be
compressed, determines the frequency of occurring characters, and assigns
shorter codes to frequently occurring characters, and longer codes to
those which occur infrequently. For example, given the observed alphabet
ABCDE, each character is determined to be a leaf node in a binary tree.
Every node in the binary tree will contain the occurrence
probability of one of the characters belonging to this subtree. In
figure 2 below, the characters A, B, C, D, and E have the following
probability of occurrence (based on observation of the data stream):
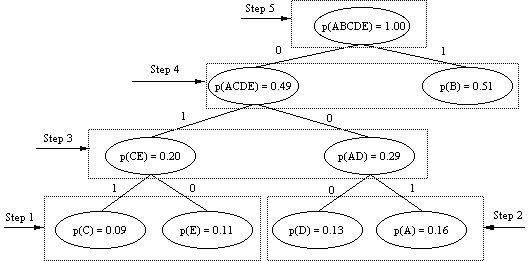
p(A) = 0.16, p(B) = 0.51, p(C) = 0.09, p(D) = 0.13, p(E) = 0.11
(NB: the probabilities are normalized.)
Characters with the lowest probabilities are combined in the first binary
tree (Step 1 in the figure). The next two nodes with the lowest
probabilities are combined into the next binary subtree (step 2). This
process continues until all the remaining nodes have been combined into
subtrees. The allocation of binary 1 and 0 to the paths is arbitrary. The
Huffman table used for encoding a bit stream must be available to the
decoder. Huffman coding is optimal, and guarantees a minimal encoded data
stream. Images are usually represented at the pixel level, and each pixel may be
represented by 8, 16, or 24 bits, depending on the colour-depth. However,
patterns may emerge within the byte representation of pixels. In
order to take advantage of Huffman coding, the pixel representation must
first be transformed into a bit-stream. It is then possible to obtain a
minimal stream length by applying the Hoffman algorithm. The resulting Huffman
table must be available to the decoder to reproduce an image identical to
the original. If the source is a video (a sequence of images), then each
frame may be encoded individually, or else they may be grouped, or the
entire video stream is encoded using the same Huffman table.
Transformation encoding
Algorithms such as Discrete Cosine Transformation and Fast Fourier
Transformation
transform the data representation from one mathematical domain (e.g., time)
to another which is more suitable for compression (e.g., frequency). The
inverse transformation must exist and be known to the decoding process.
Differential encoding
Differential encoding is an important feature of techniques used in
multimedia systems. In this technique, features of the source data (e.g.,
an image) are used to calculate the difference between, say, adjacent
pixels. For example, neighbouring pixels which together form the
background of an image are likely to have identical intensity values.
Instead of encoding each pixel value as using 3 bytes, differential
encoding would store the value of 1 of the pixels and then difference of the other
pixels could be stuffed into individual bits (if their differential value
is 0). Run-length encoding can then be performed to further reduce the
length of the data stream. In video, this technique could be used to store
a frame (known as a key-frame) in its entirety, with subsequent frames being
encoded using only the differences from the key-frame. The same techniques
can be applied to motion vectors - as an object "moves" across the screen,
there will be groups of pixels which differ from frame to frame only by
their location in subsequent frames. With audio, subsequent samples are
stored only as differences from the previous sample, as it is likely
(especially with voice transmissions) that only minor differences will
occur in a sequence (Differential Pulse Code Modulation). Audio can be
further compressed using silence suppression - data is only encoded if the
volume level exceeds a certain threshold.
JPEG
In 1982, Working Group 8 of the International Standards Organization began
working on the standardization of compression and decompression of still
images. In 1986, the Joint Photographers Expert Group (JPEG) was formed,
and in 1992, JPEG became an ISO standard.
The need for image compression is evident in the following example. A
typical digital image has 512x480 pixels. In 24-bit colour (one byte for
each of the red, green and blue components), the image requires 737,280
bytes of storage space. It would take about 1.5 minutes to transmit the
uncompressed image over a 64kb/second link. The JPEG algorithms offer
compression rates of most images at ratios of about 24:1. Effectively,
every 24 bits of data is stuffed into 1 bit, giving a compressed file size
(for the above image dimensions) of 30,720 bytes, and a corresponding
transmission time of 3.8 seconds.
Overview of JPEG
Although JPEG is one algorithm, in order to satisfy the requirements of a
broad range of still-image compression applications, it has 4 modes of
operation.
Sequential DCT-based
In this mode, 8x8 blocks of the image input are formatted for
compression by scanning the image left to right and top to bottom. A block
consists of 64 samples of one component that make up the image. Each block
of samples is transformed to a block of coefficients by the forward
discrete cosine transform (FDCT). The coefficients are then quantized and
entropy-encoded.
Progressive DCT-based
This method produces a quick low-resolution version of the image, which is
gradually (progressively) refined to higher resolutions. This is
particularly useful if the medium separating the coder and decoder has a
low bandwidth (e.g., a 14.4K modem connection to the Internet, in turn
providing a slow connection to a remote image database). The user can stop
the download at any time. This is similar to the sequential DCT-based
algorithm, but the image is encoded in multiple scans.
Lossless
The decoder renders an exact reproduction of the original digital image.
Hierarchical
The input image is coded as a sequence of increasingly higher resolution
frames. The client application will stop decoding the image when the
appropriate resolution image has been reproduced.
JPEG Operating Parameters and definitions
Parameters
An image to be coded using any JPEG mode may have from 1 to 65,535 lines
and 1 to 65,535 pixels per line. Each pixel may have 1 to 255 components,
although progressive mode supports only 1 to 4 components.
Data interleaving
To reduce the processing delay and/or buffer requirements, up to four
components can be interleaved in a single scan. A data structure called
the minimum-coded unit has been defined to support this
interleaving. An MCU consists of one or more data units, where a data unit
is a component sample for the lossless mode, and an 8x8 block of component
samples for the DCT modes. If a scan consists of one components, then its
MCU is equal to one data unit. For multiple component scans, the MCU
contains the interleaved data units. The maximum number of data units per
MCU is 10.
Marker codes
Different sections of the compressed data stream are delineated using
defined marker codes. All marker codes being with a left-aligned hex "FF"
bytes, making it easy to scan and extract part of the compressed data
without needing to decompress it first.
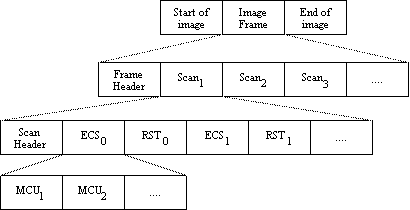
Compressed-image data structure
At the top level of the compressed data hierarchy is the image. A
non-hierarchical mode image consists of a frame surrounded by SOI and EOI
marker codes. A hierarchical coded image will have multiple frames. Within
each frame, a SOF marker identifies the coding mode used. Following an SOF
marker will be a number of parameters and one or more scans. Each scan
beings with a header identifying the components to be contained within the
scan, and more parameters. The scan header is followed by an entropy-coded
segment. The ECS can be broken into chunks of MCUs called restart
intervals, which is useful for identifying select portions of a scan, and
for recovery from limited corruption of the entropy-coded data. Quantization
and entropy-coding tables may either be included in with the compressed
image data, or be held separately.
Sequential DCT
This mode offers excellent compression ratios while maintaining image
quality. A subset of the DCT capabilities has been identified by JPEG for
a "baseline system". This section describes the baseline system.
DCT and quantization
All JPEG DCT-based coders begin by partitioning the image into
non-overlapping 8x8 blocks of component samples. The samples are level
shifted, so that their values range from -128 to +127 (instead of 0 to
255). These data units of 8x8 shifted pixel values are defined by
Sij, where i and j are in the range 0 to 7.
The blocks are then transformed from the spatial domain into the frequency
domain using FDCT:
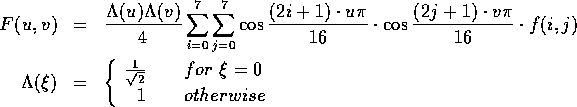
This transformation is carried out 64 times per data unit, resulting in 64
coefficients of Svu.
. The resulting
8x8 matrix will have coefficients ranging from
S00 to
S77, where
S00 is known as the DC-coefficient and
determines the fundamental colour of the data unit of 64 pixels in the
original image. The other coefficients are called AC-coefficients. To
reconstruct the image, the decoder uses the IDCT:
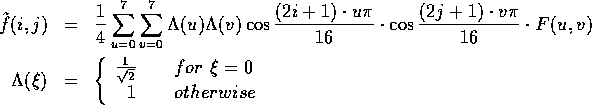
The next step to perform is quantization. The process of quantization
reduces the number of bits needed to encode data and also to increase the
number of zero-valued coefficients. For this purpose, JPEG applications can
specify a table with 64 entries, with a one-to-one mapping between the
values in the table and the DCT-coefficients. Each DCT-coefficient is
divided by its corresponding quantization value, and is rounded to the
nearest integer. JPEG does not specify a quantization table in the
standard. Applications can develop their own tables, which best suit the
type of images used. The quantization table must be available to the
decoder, or else the decoded image may be distorted. Dequantization is
performed by multiplying each DCT-coefficient by the corresponding
quantization value. Notice, however, that in the compression process, the
dividend is rounded - therefore, this technique is lossy, as the
decompression process cannot recover the original values of each pixel!
Most of the areas of a typical image contain large regions composed of the
same colour. After FDCT and quantization, the corresponding S values will have very
low values, although edges in the image will have high frequencies. On
average, images have many AC-coefficients which are almost zero. The image
is further compressed by entropy-encoding the DCT-coefficients in each
data unit.
Entropy Encoding
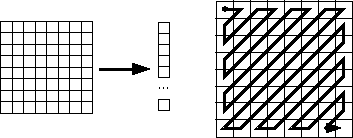
Zig-zag scan.
If a vector of quantized values is constructed using a zig-zag scan shown
in the figure above, then there will usually be a long run of zeros.
First, the zero values of the AC-coefficients are run-length coded.
Then, in the baseline system, the vector is Huffman coded. In
non-baseline systems, Huffman or the more efficient arithmetic coding
can be applied. In both cases, the Huffman or arithmetic tables must be
available to the decoder. This supports sequential encoding, where the
image is encoded and decoded in a single run.
Expanded Lossy DCT-based Mode
In addition to the method described previously, JPEG specifies
progressive encoding. Instead of using just one quantization
step, progressive encoding supports several which are applied iteratively.
Basically, the bigger the quantization block, the less definition is
encoded. So, using an 8x8 quantization table will directly match the
8x8 data blocks extracted from the image in the first place, and apart
from the rounding error, will give a fairly accurate decompressed
image. However, consider the situation where a 64x64 quantization table
is used. Now 8 8x8 blocks will be quantized at a time, resulting in a
significant loss in precision. The greater the quantization table, the
lower the overall precision of the decompressed image. However, if many
quantization tables are used and reapplied to the same
DCT-coefficients, then as the image is being decompressed, it will be
possible to gradually discern more and more definition. The major
advantage is that if the image is being downloaded over a slow network
connection, then the user can see what is in the image faster than if
the sequential encoding has been used. The user can then interrupt the
download if the image is not what s/he was expecting.
Lossless Mode
This mode is used when it is necessary to decode a compressed image
identical to the original. Compression ratios are typically only 2:1.
Rather than grouping the pixels into 8x8 blocks, data units are
equivalent to single pixels. Image processing and quantization use a
predictive technique, rather than a transformation encoding one. For
a pixel X in the image, one of 8 possible predictors is selected (see
table below). The
prediction selected will be the one which gives the best result from
the a priori known values of the pixel's neighbours, A, B, and C.
The number of the predictor as well as the difference of the prediction
to the actual value is passed to the subsequent entropy encoding.
| Selection Value | Prediction |
| 0 | No prediction |
| 1 | X=A |
| 2 | X=B |
| 3 | X=C |
| 4 | X=A+B-C |
| 5 | X=A+(B-C)/2 |
| 6 | X=B+(A-C)/2 |
| 7 | X=(A+B)/2 |
Hierarchical Mode
This mode uses either the lossy DCT-based algorithms or the lossless
compression technique. The main feature of this mode is the encoding of
the image at different resolutions. The prepared image is initially
sampled at a lower resolution (reduced by the factor
2n). Subsequently, the resolution is
reduced by a factor 2n-1 vertically and
horizontally. This compressed image is then subtracted from the
previous result. The process is repeated until the full resolution of
the image is compressed.
Hierarchical encoding requires considerably more storage capacity, but
the compressed image is immediately available at the desired resolution.
Therefore, applications working at lower resolutions do not have to
decode the whole image and then subsequently reduce the resolution.
Back to the index for this course.
In case of any difficulties or for further information e-mail
cstaff@cs.um.edu.mt
Date last amended: Friday, 26 February, 1999