| |
BACK
TO TABLE OF CONTENTS
Elementary Algebra (i)
(1) Topics coverec in this sheet
(2) Recall
(3) Exercises
Note: The solutions for the qestion no. 3b may be dowloaded from
here.
(1) Topics covered in this sheet:
-
Introduction to the f(x) notation
-
Factorisation
-
Quadratics
-
Difference of two squares
-
Difference and sum of of two cubes
-
Factor theorem
-
Soving simple equations
-
The concept of real/non-real roots
(2) Recall:
(a) Nomenclature
(i) Symbols

(ii) Sets

(iii) Numbers

(iv) Note that:
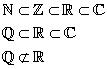
(b) Sums/Differences of two squares/cubes.
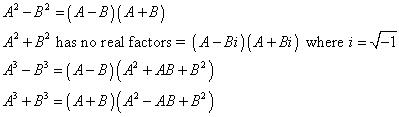
(c) Definition:
We say that f(x) is a polynomial in x
of order n when
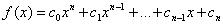
and 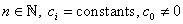 . .
(d) Factor Theorem:
-
If (x-a) is a factor of f(x) then f(a) = 0.
-
Conversly, for a given f(x) = a polynomial in x, if f(a)
= 0 then (x-a) is a factor of f(x).
(e) Real/non-real factors/roots
Consider f(x) a nth order polynomial
in x with rael cofficients ci given by:
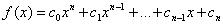
-
f(x) will have a maxium of n real roots and n
real factors.
-
f(x) may also have some complex roots. If this is the case, these
complex roots must occur in pairs of complex conjugates. The total number
of real/complex roots is always equal to n (taking into considerations
any double roots!). Thus for example:
-
A cubic may have: (i) 3 real roots, or (ii) 1 real root and two complex
roots which have to be complex conjgates.
-
A quardic may have: (i) four real roots, (ii) 2 real roots and 2
complex roots which have to be complex conjgates, or (iii) 4 complex roots,
i.e. two pairs of complex conjgates.
-
When n is ODD, we are guanateed atb least one real root. This is
not the case when n is EVEN.
(3) Qustions:
(a) Evaluate (i) f (2) , (ii) f (-1), (iii)
f
(-3)
and (iv) f (0);
(b) Factorise f(x) as completly as possible.
(c) Solve the equations f(x) = 0
... given that f(x) is given by:
|
No. |
f (x) |
|
1 |
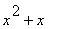 |
|
2 |
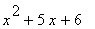 |
|
3 |
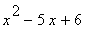 |
|
4 |
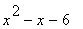 |
|
5 |
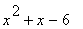 |
|
6 |
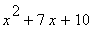 |
|
7 |
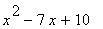 |
|
8 |
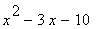 |
|
9 |
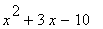 |
|
10 |
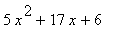 |
|
11 |
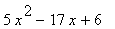 |
|
12 |
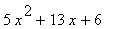 |
|
13 |
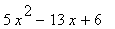 |
|
14 |
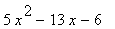 |
|
15 |
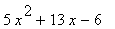 |
|
16 |
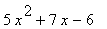 |
|
17 |
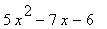 |
|
18 |
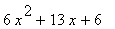 |
|
19 |
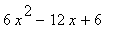 |
|
20 |
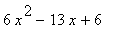 |
|
21 |
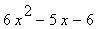 |
|
22 |
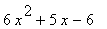 |
|
23 |
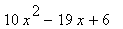 |
|
24 |
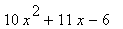 |
|
25 |
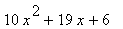 |
|
26 |
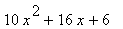 |
|
27 |
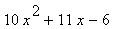 |
|
28 |
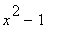 |
|
29 |
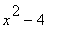 |
|
30 |
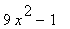 |
|
31 |
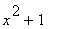 |
|
32 |
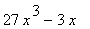 |
|
33 |
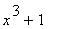 |
|
34 |
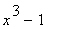 |
|
35 |
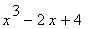 |
|
36 |
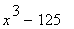 |
|
37 |
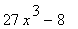 |
|
38 |
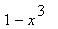 |
|
39 |
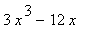 |
|
40 |
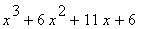 |
|
41 |
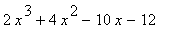 |
|
42 |
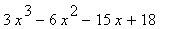 |
|
43 |
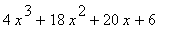 |
|
44 |
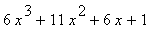 |
|
45 |
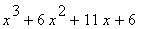 |
|
46 |
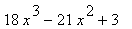 |
|
47 |
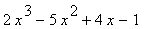 |
|
48 |
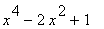 |
|
49 |
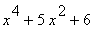 |
|
50 |
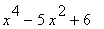 |
|
51 |
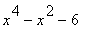 |
|
52 |
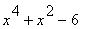 |
|
53 |
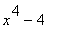 |
|
54 |
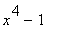 |
|
55 |
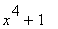 |
|
56 |
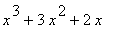 |
|
57 |
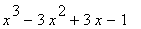 |
|
58 |
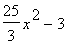 |
|
59 |
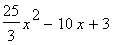 |
|
60 |
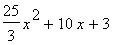 |
BACK
TO TABLE OF CONTENTS
|

