- Definition of enthalpy and enthalpy changes, H and DH
- Thermochemical equations, standard conditions and conventions of standard conditions
- Relationship between DU and DH,
- Hess's Law
- DH for various processes:
- Calculation of DH from: (i) enthalpy changes of formation (ii) bond enthalpies (iii) Hess cycles
- Enthalpy, H, is a function that describes energy changes at constant pressure.
- This means that the change in enthalpy, DH may be defined as:
- Enthalpy, H, may be defined as:
- H is a state function since, U, p, and V are all state functions.
- DH = DQ|P
= DU + pDV
....................(eqn. 1)
- H = U +pV
....................(eqn. 2)
- dH = dU + dpV + pdV
....................(eqn. 3)
dH = dU + pdV ....................(eqn. 4)
Thermochemical equations, standard
conditions and conventions of standard conditions
Thermochemical equations: In specifying the enthalpy of a reaction, special care must be taken to unsure that the states of all the reactants/products is clearly stated. This is because the enthalpy change for a reaction is dependent on the state of the reactant/products. Thus, for example, a reaction must be specified in the following format:
N2(g) + 3H2(g) -> 2NH3(g) DH = -92.2KJ mol-1Standard conditions: Since dH is a function of T and P, we need to standardise the way for quoting enthalpy and enthalpy changes. The standard conditions that we use (which are not the same as 'STP' form gases) are:
Standard Temperature = 25oc = 298.15KIn view of this we make use of the standard convention:
Standard Pressure = 1 Bar = 101325Pa
Standard State = pure compound at 1 Bar pressure. In solutions, we require 'activity = 1', i.e. relative to a standard concentration of 1M (1 mol dm-1) or a standard m
Sign convention:
DH = +ve => heat is absorbed => ENDOTHERMIC
DH = -ve => heat is evolved (given out) => EXOTHERMIC
As we saw above, DH may be defined as:
DH = DQ|P = DU + pDVThis means that DH may be regared to be the change in the internal energy DU, with an extra term 'pDV'. Let us now consider how significant this extra term is. We shall consider two scenarios:
(1) Reaction involves only solid/liquids:In this case, DV » 0 => DH »DU(2) Reaction involves gases:Assuming that a gas behaves ideally, then p(DV) = (Dn)RT. This means that the 'DV' may be significant.For example, for Dn = 1 mole (i.e. 1 more of gas is evolved), we have:
(i) At 25oc (298.15K), (Dn)RT = 2.48 kJ = p(DV)
(ii) At 500oc (773.15K), (Dn)RT = 6.43 kJ = p(DV)
These values (especially at higher temperature) are significant!!!
Hess's law states that the total enthalpy change for a reaction is independent of the path by which the reaction occurs.
Note: DH (forward) = -DH
(reverse)
[TOP]
DH for various processes:
The enthalpy of formation of a compound,
is the enthalpy change when one mole of compound is formed under standard
conditions from one mole of its constituent elements in their standard
state.
e.g.
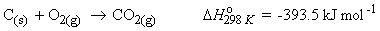

=>
The enthalpy of combustion
(or the heat of combustion) is the enthalpy change when one mole of compound
reacts completely with excess oxygen under standard conditions.
e.g.
The bond dissociation enthalpy (bond energy) represents the energy required to break one mole of chemical bonds in the gas phase. The term 'mean bond dissociation energy' is more commonly used, since the actual energy required to break a particular bond is dependent on the precise environment of the bond.
Consider the dissociation of methane by successive breakage of C-H bonds:
We have:
(i)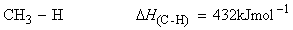
(ii)
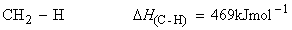
(iii)
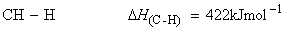
(iv)
Given this information we may estimate the mean bond dissociation
enthalpy for C-H given by:
The 'phase change' enthalpy represents the energy required/given off when one mole of pure substance changes phase. Note:
(1) DH(freezing) = - DH(fusion), etc.These are usually quoted under 1Bar pressure, at the temperature where the phase change occurs.
(2) DH(sublimation) = DH(fusion) + DH(vaporisation)
(5) Enthalpy of Solution.
The enthalpy of solution is the enthalpy associated with the process when a process enters solution. There can be different types of enthalpy of solution, the most common being:
(a) The integral enthalpy of solution - the enthalpy change when one
mole of solute dissolves in a large excess of pure solvent.
e.g. HCl(g) + (aq) -> HCl(aq) DH = 74.4kJ mol-1
(b) The differential enthalpy of solution - the enthalpy change
when one mole of solute dissolves in a large amount of solution.
e.g. DH for dissolving 1 mole of HCl(g) in 0.1M HCl is different from DH for dissolving 1 mole of HCl(g) in 1M HCl, and is different from the 74.4 kJ mol-1 quoted above.
(c) The enthalpy of hydration is reserved for the special case when
the solvent is water.
- enthalpy changes of formation
- bond enthalpies
- Hess cycles
(3) The enthalpy of a reaction can also be calculated by constructing a Hess’ cycle, i.e. by application of Hess’ Law – The standard enthalpy of an overall reaction is the sum if the sum of the individual reaction into which a reaction may be divided, and by noting that DH(forward) = -DH(reverse). In this method, a chemical reaction is re-written in terms of a number of other reactions for which we know the reaction enthalpy changes. These individual steps need not even be realizable in practice (i..e we could make use of the reverse of a reaction, and then make use of the fact that DH(forward) = -DH(reverse).). The only important requirement is that the chemical equations should balance.