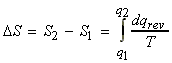Entropy - The second Law of
thermodynamics, Classius Inequality.
(1) What is entropy?
Why do we need to consider entropy? Does a reaction happen simply to minimise the energy? NO!!! - For example
(A)
Although this system absorbs heat, the reaction still happens spontaneously.
(B) Does the reverse of (A) happen by heating
(i.e. without evaporating the water)? NO!
The reason for this 'strange' behaviour is that process (A) results
in an overall increase in the disorder. To account for this we shall introduce
a new property - ENTROPY, S.
(2) Entropy and the molecular state of the system.
The entropy 'S' of a system relates to 'W', the number of ways for arranging the molecules of the system through:
where kB is Boltzmann's constant.
NOTE:
(3) The second law of thermodynamics:
Spontaneous processes are those which increase the entropy of the universe (i.e. system + surroundings).
i.e.
(positive)
(4) The Thermodynamic definition of entropy - The Classius inequality
We may define entropy thermodynamically by:
Consider two states '1' and '2'. To find the entropy change, DS between the two states '1' and '2' we :
(i) Find a reversible path for 'q' between state '1' and '2';
(ii) Integrate, i.e.
which at constant 'T' becomes:
NOTE: Dqrev is the
most energy expensive path between '1' and '2', since a reversible is the
one from which we may take most work (i.e. maximum negative work), and
entropy is a state function (i.e. DU is the
same for any route form 1 to 2). Therefor, for any process:
The Classius inequality may be proved more formally as follows:............................................... (Classius inequality)
We have shown that the entropy of a system is given by:
However this relationship is of very little practical use since:
(a) It is difficult to ensure that 'dq' refers to a reversible process;
(b) It is difficult to ensure that T is constant.
In an attempt to rectify this situation we shall consider the entropy change of the surroundings.
(a) We may consider the surroundings to be a reservoir of constant volume, i.e. that there is no p-V work. This means that dqSUR = dUSUR. But U is a state function, and hence a change in U is independent of the path. In particular it is independent of whether the path is reversible or irreversible. This means that for the surroundings, 'dqSUR' is always equivalent to 'dqSUR,rev'.
(b) Since the surroundings are very large we may assume that T is constant.
This means that:
But from the second law of thermodynamics,
i.e.:
But, ,
that is if we assume that there is perfect thermal contact between the
system and the surroundings, we have:
i.e.:
………………. (CLASSIUS INEQUALITY)
NOTE: If system is isolated, then dq = 0, i.e. the Classius
inequality reduces to: