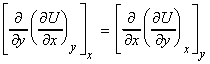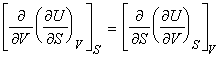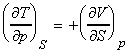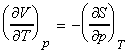Combining the first and second laws of thermodynamics - The fundamental equations of thermodynamics
(1) The fundamental equations of thermodynamics
The first law of thermodynamics may be written as:
where for a reversible change a closed system of constant composition, and in the absence of non-expansion work we have:
Therefore we may re-write the first law as: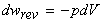
THIS REALTIONSHIP IS KNOWN AS THE FUNDAMENTAL EQUATION OF THERMODYNAMICS .
We will revisit this equation at a later stage to include the effects of changing the composition of the system (the fundumental equation of chemical thermodynamics.)This equation shows how the internal energy of a closed system changes with changes in S and V, i.e. U = U(S,V). Now, because dU is an exact differential (U is a state function), its value is path independent, i.e. this equation is valid for all types of processes of a closed system that does no non p-V work.
(2) Use of the Fundamental Equation to generate new functions (Derivations not examinable.)
If we where to differentiate U = U(S,V) we get:
i.e. from the fundamental equation we see that:
and
Another very interesting equation (one of a set called the Maxwell relationships) may be obtained from the property that if for U = U(x,y) , dU is an exact differential, then we have:
which in our case we have:
i.e.:
or:
NOTE: The full set of the Maxwell relationships may be derived form
the other thermodynamic functions and are summarised as follows (not examinable):