- Definition of the Helmholtz free energy and the Gibbs free energy.
- The free energy and chemical reactions
- The relationships between the free energies and entropy, enthalpy, and the internal energy.
- The free energies and the concept of maximum work
> System in thermal equilibrium with surroundings at a temperature T
> There is a change in the system accompanied by a transfer of energy dq between system and surroundings
> From the Classius Inequality we have:
i.e.:
or:
This inequality may be developed in two ways:
(a) Under the conditions of constant volume we have no p-V work,
i.e. in the absence of other forms of work:
i.e.:......................... (constant V, no non-expansion work)
(b) Under the conditions of constant pressure, in the absence of other forms of work other than p-V, we have :
i.e.:......................... (constant p, no non-expansion work)
The two inequalities above (i.e.
and 
) and
are so important (they determine whether a process is going to occur or
not) that we shall assign to them two new thermodynamic functions namely:
(a) The Helmholtz free energy, A, given by:
(b) The Gibbs free energy, G, given by:
These two functions may be differentiated to give:
Which at the conditions of constant temperature T, we have: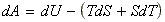
Thus the two inequalities above (i.e. 
and 
) governing the conditions
for a spontaneous process may be summarised as:
.........................(from
)
.........................(from
)
Note that 
and 
refer
to conditions at equilibrium.
DG plays a very important role in standard laboratory conditions are usually under constant pressure and temperature.
For practical reasons, the standard Gibbs free energy for a reaction
is defined in terms of the standard Gibbs energies of formation, DfG0,where
The
standard Gibbs energy of formation is the standard reaction Gibbs energy
for the formation of a compound from its elements in their reference states.
(Standard
Gibbs energies formation of the elements in their reference states are
zero, because their formation is 'null' reaction.),as follows:
NOTE: The proper definition of the standard Gibbs
energy of reaction is the difference in standard molar Gibbs energies the
products and reactants in their standard states at the temperature specified
for the reaction as written.
The standard Gibbs free energy relates to the reaction enthalpy and entropy as follows:
The experimental values of DrG0 are obtained either through calorimetric methods (finding DH directly, and DS from the heat capacities), or through equilibrium constants (discussed at a later stage). Other methods are also possible.
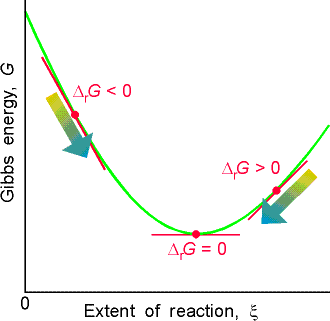
The spontaneity of a reaction at constant temperature and pressure is
related to the Gibbs free energy as follows (see Fig. 1):
(i) IfSimilar arguments may be presented for DA.(exergonic, from the Greek word for work-producing), the forward reaction is spontaneous.
(ii) If
(endergonic, signifying work-consuming), the reverse reaction is spontaneous.
(iii) If
, the reaction is at equilibrium.
|
(3) The relationships between the free energies and entropy, enthalpy, and the internal energy.
(a) From both inequalities, it may be clearly deduced that a positive dS favours the spontaneity of the process (i.e. a negative dA or dG)
(b) From the inequality at constant volume, we may deduce that a negative dU favours a negative dA. The interpretation for this should be that a process with a negative dU is accompanied by a positive entropy change of the surroundings, given by '-dU / T ' (i.e. the spontaneity is not driven by the desire for a lower value of dU, but for a higher value of dSSUR. ) Systems change spontaneously if the total entropy (system + surroundings) increases, not because they tend to a lower internal energy.
(b) Note that endothermic reactions do occur provided that 
.
Such reactions happen because the entropy increase in the system is greater
than the entropy decrease of the surroundings (
).
(4) The free energies and the concept of maximum work
(a) The change in the Helmholtz free energy is equal to the maximum work accompanying a process, i.e.:
Because of this, A is sometimes called the 'maximum work function' or the 'work function' (Arbeit is the German word for work, hence the symbol A). We can show this by combining the first law with the Classius inequality -
i.e.:
This means that the most negative value of dw (i.e. the most
amount of work that we can extract from a system) is given by:
which at constant temperature is equal to dA. This equation
suggests that the amount of energy available for work maybe less than the
internal energy (if TDS < 0).
(b) In analogy, dG refers to the maximum non-expansion work.
(See Atkins, p. 117).
 |
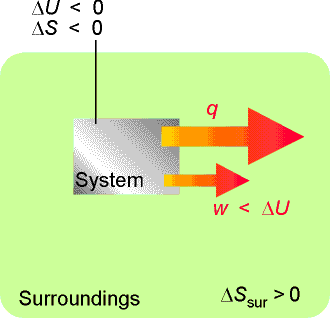In a system not isolated from its surroundings, the work done may be different from the change in internal energy. Moreover, the process is spontaneous if, overall, the entropy of the global, isolated system increases. In the process depicted here, the entropy of the system decreases, so that of the surroundings must increase in order for the process to be spontaneous, which means that energy must pass from the system to the surroundings as heat. Therefore, less work than |DU| can be obtained. |
 |
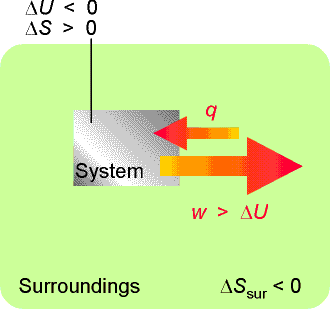In this process, the entropy of the system increases; hence we can afford to lose some entropy of the surroundings. That is, some of their energy may be lost as heat to the system. This energy can be returned to them as work. Hence the work done can exceed DU. |