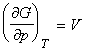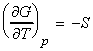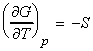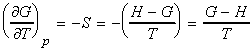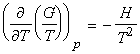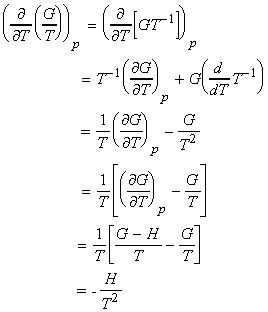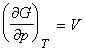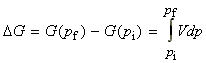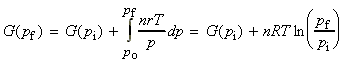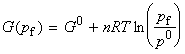Properties of the Gibbs free energy
- The temperature dependence of the Gibbs free energy (The Gibbs-Helmholtz equation.)
- The pressure dependence of the Gibbs free energy,
Properties of the Gibbs free energy
We have defined the Gibbs free energy G and the enthalpy H as:
and hence: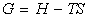
i.e.: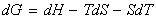
But for a system doing no non-expansion work, dU may be replaced by the fundumental equation of thermodynamics, i.e.:
and hence we have:
which simplifies to:
which since dG is an exact differential gives us:
and:
These relationships show that G varies with temperature and
pressure
(1) The temperature dependence of the Gibbs free energy (The
Gibbs-Helmholtz equation.)
The temperature dependence of G is governed by the following relationship:
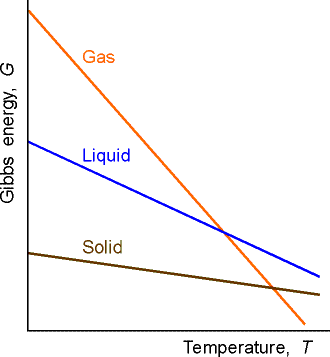
This means that because S is positive, then G decreases when the temperature increases at constant pressure (G vs T plot, see fig. 1).
Then sharpness of the decrease of G decreases with temperature at constant pressure is determined by the entropy of the system. This means that the sharpness of the decrease of the G vs T (i.e. the sensitivity of G with changes in T, = gradient of G vs T plot, see fig. 1) is greatest for a gas, then liquid, then solid.
Let us now derive a relationship between the Gibbs energy and enthalpy (The Gibbs-Helmholz equantion). From the definition of G , we have:
i.e.:
i.e.:
which simplifies to the Gibbs-Helmholtz equation (see proof below):
The Gibbs-Helmholtz equation is most useful when applied to changes, including change of phase or chemical reactions at constant pressures. Then since DG = Gf - Gi, and since the Gibbs-Helmholtz equation applies to both Gf and Gi, we can write:
Fig. 1: The variation of the Gibbs energy with the temperature is determined by the entropy.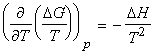
Aside: Proof of the Gibbs-Helmholtz equation:
(2) The pressure dependence of the Gibbs free energy
The pressure dependence of G is governed by the following relationship:
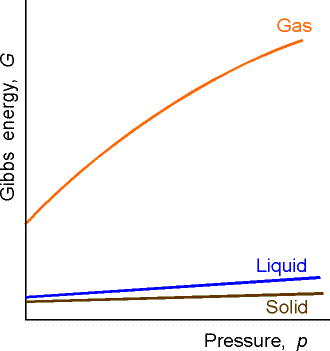
This means that because V is positive, then G always increases when the pressure increases at constant temperature (G vs p plot, see fig. 2). Also, since V is the gradient of the G vs p plot, then the sensitivity of G to changes in p is greatest for gases and negligible for liquids and solids (see fig. 2).
Fig. 2: The variation of the Gibbs energy with the pressure
We can find the change in the Gibb's energy due to a change in pressure at constant temperature through:
For solids and liquids, we then treat V as constant, whilst for an ideal gas we use the pV=nRT relationship, and we get:
or if we assume pi = p0 then we get: