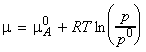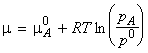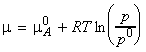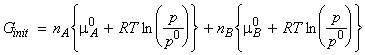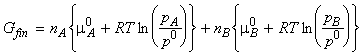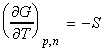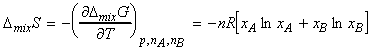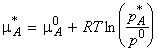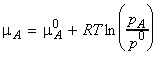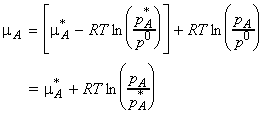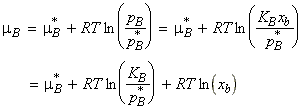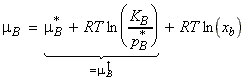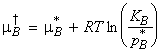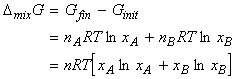(1-1) The chemical potential of gaseous solutions(2) Liquid mixtures
(1-2) The Gibbs energy, entropy and enthalpy of mixing for gases
(2-1) The chemical potential of ideal liquid solutions
(2-2) The chemical potential of ideal-dilute liquid solutions
(2-3) The chemical potential of real liquid solutions - activities
(2-4) The Gibbs energy, entropy and enthalpy of mixing for liquids
(2-5) Colligative properties
(1-1) The chemical potential of a component in a gaseous mixture
We have seen that for pure A, the chemical potential is given by:
where p is the pressure of the gas. If another substance B is added to A, then the chemical potential of A in the mixture is given by:
where pA is the partial pressure of A in the mixture.
The Gibbs free energy of mixing -
We have seen that for a binary system:
and that for pure A, (and similarly for B), the chemical potential is given by:
Thus let us assume that we start with two pure gases A and B (amounts nA and nB respectively) in two separate containers at the same temperature T and pressure p. At this stage, the gases have their 'pure' chemical potential, and hence, the total initial Gibbs energy whilst they are still in separate containers is given by:
When we mix the gases, the pressures 'p' have to be replaced by their partial pressures in the mixture, i.e. pA and pB where pA = pB = p. The total Gibbs energy then changes to:
and hence:
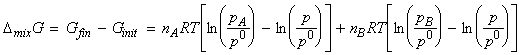
i.e.:
[why?]
But, (i) nJ=xJ n , and (ii) from Dalton's law, pJ / p = xA . Hence we have:
Note that since xJ are always less than 1, ln(xJ) are always negative and hence for all perfect gasses, and in all proportions, DmixG < 0 and hence gases mix spontaneously.
The entropy of mixing can be calculated from a corollary of the fundamental equation of thermodynamics, i.e.:
and hence:
i.e. DmixS > 0 for
all compositions since ln(xA) and ln(xB)
are both negative since xA and xB are
necessarily less that 1 (see graph of ln(x))
The enthalpy of mixing (isothermal and isobaric) of two perfect gases may be calculated from:
which gives:
as expected since the molecules of perfect gases do not interact.
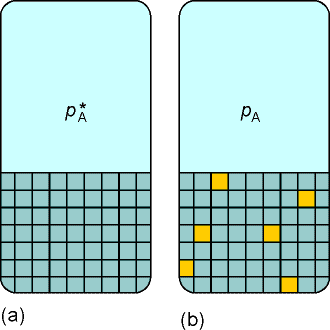
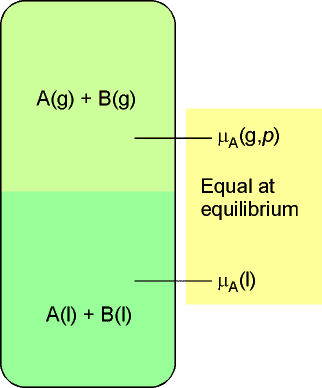
The basis for this discussion shall be that the chemical at equilibrium,
the chemical potential of a substance present as a vapour must be equal
to its chemical potential in the liquid, as illustrated
in Fig. 1 below.
(2-1) The chemical potential of ideal liquid solutions - Raoult's
law
In this discussion we shall make use of the superscript * to denote
that the chemical potential refers to the pure substance. The chemical
potential of pure A is written as if
we need to distinguish between the liquid phase or the vapour (gas) phase.
The vapour pressure of the pure liquid A is hence written as
.
The chemical potential of A (in liquid and in the vapour) is given by
where:
If another substance (a solute, B) is also present in the
liquid, then we must replace the chemical potential and vapour pressure
of the pure liquid by the partial chemical potential and the partial vapour
pressure, i.e.:
We can combine these two equations to eliminate
 ,
to give:
,
to give:
In the case of an ideal solution, when both
the solute and solvent obey Raoult's law (for closely related liquids,
the ratio of the partial pressure of each component to its vapour pressure
as a pure liquid is approximately equal to the mole fraction in the liquid
mixture, see Fig. 2a/b for a graphical illustration), i.e.:
We have:
Note: Even when solutions depart significantly from Raoult's law (Fig. 2c/d), the relationship for the chemical potential is obeyed increasingly closely for the solvent (i.e. the component in xs) in the limit of infinite dilution.
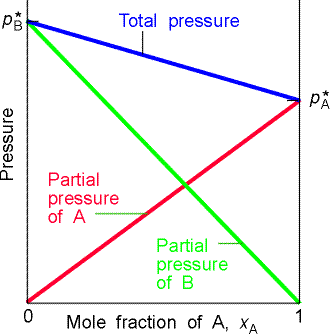
(a) The total vapour pressure and the two partial vapour pressures of an ideal binary mixture are proportional to the mole fractions of the components. |
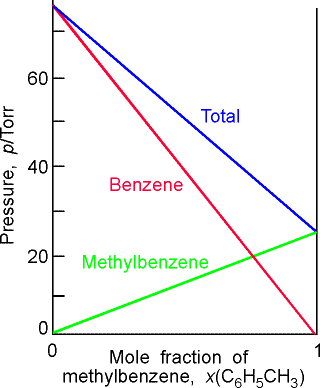
(b) Two similar liquids, in this case benzene and methylbenzene (toluene), behave almost ideally, and the variation of their vapour pressures with composition resembles that for an ideal solution. |
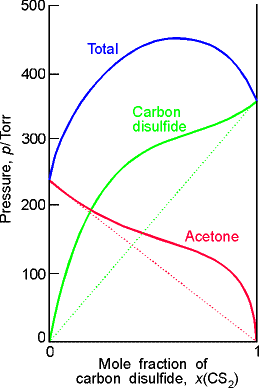
(c) Strong deviations from ideality are shown by dissimilar liquids (in this case carbon disulfide and acetone (propanone)). |
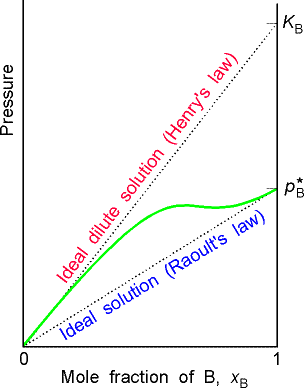
(d) When a component (the solvent) is nearly pure, it has a vapour pressure that is proportional to the mole fraction with a slope p*B (Raoult's law). When it is the minor component (the solute), its vapour pressure is still proportional to the mole fraction, but the constant of proportionality is now KB(Henry's law). |
Fig. 2- Vapour pressure vs. composition diagrams
(2-2) The chemical potential of ideal-dilute solutions - Henry's
law
William Henry had found that for real solutions at low concentrations, (a) the vapour pressure of the solute, pB , is proportional to the mole fraction, xB , and that (b) the constant of proportionality, KB , is not the vapour pressure of the pure substance (as in Raoult's law), but has to be determined experimentally (the tangent of pBvsxB in the limit of xb = 0). This discovery is better known as Henry's law. (In other worksm Henry's law says that: " pB = KB xB " . )
Henry's law is particularly useful for obtaining the chemical potential of the solute in ideal-dilute solutions (which is well described by the Henry's law), since in this case:
Since both p*B and KB are characteristic of the solute rather than the mixture, we may define a new standard chemical potential, m†:
i.e.:
i.e.:
(2-3)The chemical potential of real liquid solutions - activities
From the discussion for ideal / ideal dilute liquid solutions above, we may deduce that:
(1) The equation for the chemical potential of A in terms of the vapour pressures holds for both real and ideal solutions:
………………… (eqn. 1)
(2) However, the equation for the chemical potential of A in
terms of the mole fraction, holds only for ideal solutions (ones that obey
Raoult's law):
………………… (eqn. 2)
(3) We may replace the term 'xA' (the mole fraction)
by a new term 'aA' (the activity of A, a kind of an 'effective'
mole fraction, in analogy with the fugacity), so that the for the chemical
potential retains the same simple format as in eqn. 2, i.e.:
………………… (eqn. 3)
This equation now hold for both real and ideal liquid solutions.
Note that by comparing eqn. 1 and eqn. 3, we find that:
………………… (eqn. 4)
We may hence determine the activity experimentally by measuring
the vapour pressures and then applying eqn. 4. In the limit of infinite
dilution, the activity approaches the mole fraction (since all solvents
obey Raoult's law at infinite dilution), i.e.:
(4) As in the case of the fugacity for real gases, we may introduce
the activity coefficient g, defined by:
In this case, the chemical potential of the solvent may be written
as:
(5) In the case of the solute in real solutions, we make use of
the equation for the ideal-dilute solution, with activity instead of mole
fraction, i.e. :
In this case, the activity is given by:
where KB is the empirical constant in Henry's
law.
NOTE: The composition of mixtures is often expressed as molalities,
b,
rather that mole fractions. This is discussed in P.W. Atkins, Physical
Chemistry, 6th Edn., 1998 (OUP), pg. 185-186.
(2-4) The Gibbs energy, entropy and enthalpy of mixing for liquids
Ideal solutions
As in the case of gasses, let us assume that we start with two pure liquids A and B (amounts nA and nB respectively) in two separate containers at the same conditions. At this stage, these liquids have their 'pure' chemical potential, and hence, the total initial Gibbs energy whilst they are still in separate containers is given by:
When we mix the liquids, the chemical potentials of the pure A and
B liquids have to be replaced by the chemical potentials of A and B in
solution, i.e. the total Gibbs energy changes to:
and hence the Gibbs free energy of mixing for an ideal liquid
solution:
as in the case of a mixture of ideal gases. Similarly, the entropy
of mixing and the enthalpy of mixing for an ideal liquid
solution are given by:
and:
Real solutions vs. ideal solutions
As indicated above, the DmixG obtained for an ideal binary liquid solutions is the same as that for two perfect gases. Also, as in the case of ideal gases: (i) the driving force for mixing is the increasing entropy of the system when the molecules mingle, and, (ii) the enthalpy of mixing is zero.
It should be noted, however solution ideality in liquids means something different from gas perfection. In a perfect gas there no interactions between molecules. In ideal solutions there are interactions, but the average A-B interactions in the mixture are the same as the average A-A and B-B interactions the pure liquids.
Real solutions are composed of particles for which A-A, A-B, and B-B interactions are all different. Not only may there be an enthalpy change when liquids mix, but there may also be an additional contribution to the entropy arising from the way in which the molecules **: one type might cluster together instead of mingling freely with the others. If the enthalpy change is large and positive or if the entropy change is adverse (because of a re-organization of the molecules that results in an orderly mixture), then the Gibbs energy might be positive for mixing. In that case, separation is spontaneous and the liquids may be immiscible. Alternatively, the liquids might be partially miscible, which means that they are miscible only over a certain range of compositions.
The thermodynamic properties of real solutions may be expressed in terms of the excess functions, XE, defined as the difference between the observed thermodynamic function of mixing and the function for an ideal solution. For example, the excess enthalpy, HE , the excess volume, VE and the excess entropy, SE, are defined as:
Deviations of the excess enthalpy from zero indicate the extent to which the solutions are non-ideal.
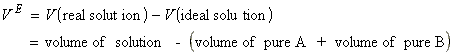
NOTE: In this connection a useful model system is the
regular solution, a solution for which HEis not zero,
but SE = 0. A regular solution can be thought of as one
in which the two kinds of molecules are distributed randomly (as in an
ideal solution) but have different energies of interactions with each other.
(2-5) Colligative properties
The presence of a solute can produce very interesting effects such as:
- Elevation of boiling point,
- Depression of freezing point
- Osmotic pressure
All the colligative properties stem from the reduction of the chemical potential of the liquid solvent as a result of the presence of solute. The reduction is from mA* for the pure solvent to mA* + RT ln xA when a solute is present (ln xA is negative because xA < 1). There is no direct influence of the solute on the chemical potential of the solvent vapour and the solid solvent because the solute appears in neither the vapour nor the solid. The reduction in chemical potential of the solvent implies that the liquid-vapour equilibrium occurs at a higher temperature (the boiling point is raised) and the solid-liquid equilibrium occurs at a lower temperature (the freezing point is lowered), as illustrated in the figure below.
The molecular origin of the lowering of the chemical potential is not the energy of interaction of the solute and solvent particles, because the lowering occurs even in ideal solutions (which have zero enthalpy of mixing). If it is not an enthalpy effect, then it must be an entropy effect. The pure liquid solvent has an entropy that reflects the disorder of its molecules. Its vapour pressure reflects the tendency of the solution towards greater entropy, which can be achieved if the liquid vaporizes to form a more disordered gas. When a solute is present, there is an additional contribution to the entropy of the liquid, even in an ideal solution. Because the entropy of the liquid in the solution is already higher than that of the pure liquid, there is a weaker tendency to form the gas. The effect of the solute appears as a lowered vapour pressure, and hence a higher boiling point. Similarly, the enhanced molecular randomness of the solution opposes the tendency to freeze. Consequently, a lower temperature must be reached before equilibrium between solid and solution is achieved. Hence, the freezing point is lowered.
Colligative properties are discussed in more detail in another study unit.