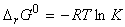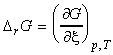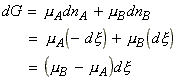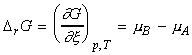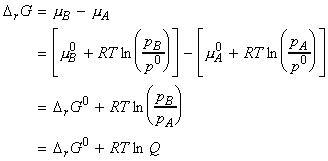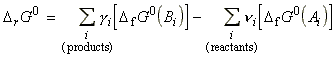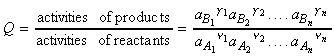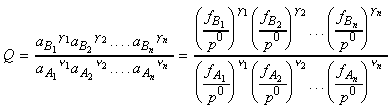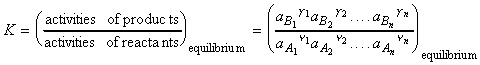(iii) Chemical reactions and equilibria - Part I
(1) Reaction Gibbs energy and equilibria
In this last section of classical thermodynamics we shall continue
to discuss how the direction of a spontaneous change (chemical reactions,
in particular) at constant pressure and temperature is directed towards
lower values of the Gibbs energy, G.
The reaction Gibbs energy, DrG is defined as the slope of the graph of the Gibbs energy, G, vs. slope of extent of reaction, x, i.e.:
This definition shows that unlike many other D'X' terms, the DrG is a gradient, and not just a simple 'change' (see below). This difference is important as the value of DrG is a function of the extent of reaction, and not simply.
For a reaction A -> B, the term DrG may be expressed in terms of the chemical potentials of A nd B as follows:
i.e.:
It is important to recall that the chemical potentials vary with composition, and hence as the reaction proceeds, and the composition varies, mB - mA changes, and hence the slope of G vs. x changes.
In particular, for the reaction A -> B, we have:
| Chemical potential | Gibbs energy | Interpretation | Name |
| mA > mB | DrG < 0 | Forward reaction (A -> B) is spontaneous | exergonic |
| mB > mA | DrG < 0 | Reverse reaction (B -> A) is spontaneous | endergonic |
| mB = mA | DrG = 0 | Reaction is at equilibrium , i.e. spontaneous in neither direction | - |
Let us now consider the simple case when A and B are both perfect gasses. We may thus write:
where:
Q is the reaction quotient which ranges from 0 (pure A) to infinity (pure B)
DrG0 is the standard reaction Gibbs energy, defined simply as the difference in the standard Gibbs molar energies of the products and reactants, or as the difference of the standard Gibbs energy of formation of products and reactants, i.e. in our case:
or:
At equilibrium we have: (i) DrG = 0, (ii) The ratio of the partial pressures may be denoted by K, 'the equilibrium constant', i.e.:
which rearranges to:
These reactions may be generalised as follows:
where: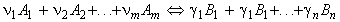
and:
or for gasses:
where fJ is the fugacity of gas J defined as aJ = fJ / p0 . Note that for perfect gasses, fJ = pJ. Note that at low overall pressures, the fugacities may be replaced by the partial pressures.
At equilibrium we have:
where K is the thermodynamic equilibrium constant (because it is expressed in terms of activities rather than concentrations, or fugacities rather than partial pressures)