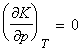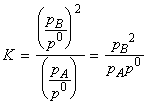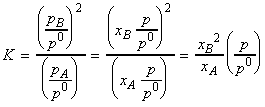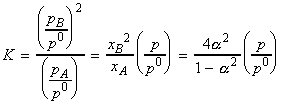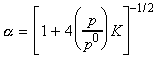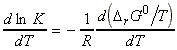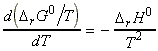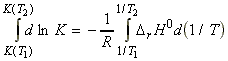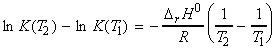(iii) Chemical reactions and equilibria - Part II
(2) Response of equilibria to external disturbances - The Le Chatelier's principle
(2-1) Response of equilibria to pressure
(2-2) Response of equilibria to temperature (van't Hoff equation)
The response of equilibria to external disturbances are governed by a very simple, and simple empirical law, proposed by the French Chemist Henri Le Chatelier, now commonly known as Le Chatelier's principle, which sates that:
A system at equilibrium, when subjected to a disturbance, responds in a way that tend to minimise the effect of the disturbance.
Such changes are of course very important as they directly effect the yield of the reaction.
Thus for example, for the generalised equation for a reaction at equilibrium:
(i) if we were to increase the number of A molecules, the would equilibrium would shift to the right, hence favouring the formation of B, and,
(ii) if we were to increase the temperature, as the forward reaction is exothermic, then the equilibrium would shift to the left, hence favouring the formation of A.
NOTE: In general, the equilibrium constant is unaffected by the introduction of a catalyst.
Let us now have a more detailed look at how equilibria are effected
by (1) pressure, and (2) temperature.
The equilibrium constant depends on the value of DG0
(
) which is defined at a single, standard pressure.
The value of DG0 and hence of K,
is therefore independent of the pressure at which the equilibrium is actually
established, or more formally:
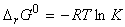
However, this conclusion that K is independent of pressure does not necessarily mean that the equilibrium composition is independent of the pressure. In fact, we are still subjected to Le Chatelier's rule if the amount of gases are not the same in the two sides of the equation. However, even in such cases, not all changes in pressure will result in the same effect. In fact:
There are two ways in which pressure can be applied:
(1) The pressure within a reaction vessel can be increased by injecting an inert gas into it. In this case, provided the gases are perfect, this addition of an inert gas leaves the partial pressures of the reacting species unchanged (i.e. the molar concentrations of the original gases are unchanged, as they continue to occupy the same volume). Thus, this type of pressurization has no effect on the equilibrium composition of the system (provided the gases are perfect).
(2) The pressure of the system may be increased by confining the gases to a smaller volume (that is, by compression). In this case, the partial pressures are changed (i.e. the molar concentrations are modified because the volume the gases occupy is reduced) and hence the equilibrium composition is effected. For example, in the general case of:
we have:
if the pressure is increased by decreasing the volume, then the equilibrium composition will shift in favour of A at the expense of B in accordance with Le Chatelier's principle. In fact, we have:
i.e. for example, 10-fold increase in the pressure will result in a 10 fold increase of the
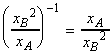ratio.
Another way of expressing this result is in terms of a, the extent of dissociation of A into B. In this case we have:
| initially | at equilibrium | |
| amount of A | n | (1-a)n |
| amount of B | 0 | 2an |
| xA , mole fraction of A | 1 |  |
| xB , mole fraction of B | 0 |  |
The equilibrium constant K is thus given by:
which shows very and hence the extent of dissociation is given by:
As we have discussed above, from Le Chatelier's principle we may deduce that:
(i) For exothermic reactions, an increase in temperature will favour an increase in the reactants;
(ii) For endothermic reactions, an increase in temperature will favour an increase in the products.
These results may be expressed quantitatively through the van't Hoff equation, an expression for the slope of ln K vs. temperature, and is usually written in one of these forms:
since:or
i.e.:
Differentiation with respect to T gives:
But from the Gibbs-Helmholtz equation, we have:
i.e.:
Also,
and hence:
NOTE: From this equation we may derive an expression for the value
of K at different temperatures as follows:
Assuming that DrH0 is constant in the region (T1,T2) then we may write*:
(*) If we do not assume that DrH0 is constant in the region (T1,T2), then we would have to re-write is DrH0 in terms of Dcp.
Let us now have a look at the significance of the van't Hoff equation, i.e.:
This equation shows that shows that d ln K / dT < 0
(negative) for an exothermic reaction under standard conditions.
This is equivalent to saying that dK / dT < 0 for exothermic
reactions under standard conditions, which means that K decreases
as the temperature rises. This confirms our statement that for exothermic
reactions, the equilibrium shifts away from products with an increase in
temperature. The opposite occurs in the case of endothermic reactions.
Some insight into the thermodynamic basis of this behaviour can be found in the expression DG = DH - TDS written in the form DG/T = DH/T + DS. The term DH/T is directly related to the change in entropy of the surroundings, since:
Thus:
- An exothermic reaction results in an increase in the entropy of the surroundings, whilst
- An endothermic reaction results in a decrease in the entropy of the surroundings (For an endothermic reaction to occur, there must be an increase in the entropy of the system, which should be big enough to cancel the decrease in entropy of the surroundings).
In contrast, when the reaction is endothermic, the principal factor
is the increasing entropy of the reaction system. The importance of
the unfavourable change of entropy of the surroundings is reduced if the
temperature is raised (because then DH /
T is smaller), and the reaction is able to shift towards products.