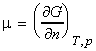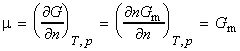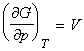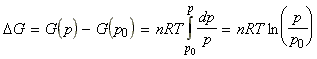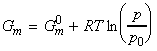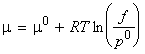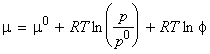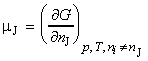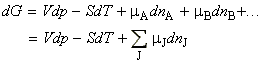(i) Chemical Potential
- (a) Chemical potential for pure substance:
(i) pure ideal gases
(ii) pure liquid
(iii) pure real gases.
In this section we shall introduce the concept of chemical potential 'm' and we shall first consider the chemical potential of a pure substance and then, that of the particular case when the substance is a perfect gas.
The chemical potential 'm' of a pure substance is defined as:
and describes how the Gibbs free energy of a system changes as a substance is added to it.
Thus for a pure substance, the Gibbs free energy is given by:
where Gm is the molar Gibbs free energy. This means that the chemical potential of a pure substance is simply Gm since:
Let us now derive an expression for Gm for a prefect gas (pure substance) at a pressure p.
We have already seen that the fundamental equation of thermodynamics for a pure substance is given by:
that is at constant T:
i.e.:
dG = V dpThus for n moles of a perfect gas, pV=nRT, i.e.:
which for a change in pressure from p0 (= 1 atm) to p, we have:
Thus, for one mole of pure gas (n=1), the molar Gibbs energy Gm is given by:
or in terms of the chemical potentials:
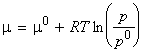 |
where m0 is the standard chemical potential, that is the molar Gibbs free energy of the pure gas at 1 bar (=p0) of the pure gas.
(ii) Chemical potential for pure liquids
At equilibrium, the chemical potential of a substance present as a vapour is equal to its chemical potential in the liquid. This means that the chemical potential of a pure liquid is given once again by:
where m0 is the standard chemical potential, and p is now the vapour pressure of the liquid.
(iii) Chemical potential for real gases
Before we can discuss real gases, we need to introduce a new term, namely the fugacity, f, a property which will replace the true pressure of the gas by an effective property. We may then write:
A plot of the chemical potential for an ideal and real gas is shown in Fig. 1.
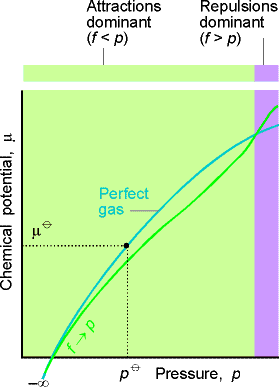
Fig. 1: The chemical potential of a real gas. As p approaches
0, m coincides with the value for a perfect
gas (shown by the pale line). When attractive forces are dominant (at intermediate
pressures), the chemical potential is less than that of a perfect gas and
the molecules have a lower `escaping tendency'. At high pressures, when
repulsive forces are dominant, the chemical potential of a real gas is
greater than that of a perfect gas. Then the `escaping tendency' is increased.
Note that the fugacity may be written as:
where f is the dimensionless fugacity coefficient, and depends on the identity of the gas, temperature and pressure. In this case, the equation for the chemical potential for a real gas becomes:
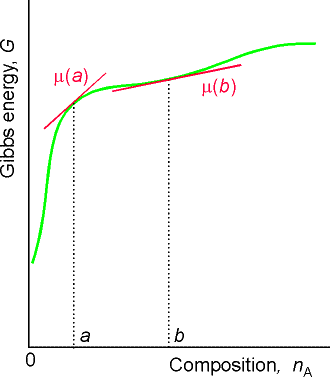
For a substance J in a mixture, the chemical potential mJ is defined as the partial molar Gibbs free energy, i.e.:
that is, the chemical potential is the slope of Gibbs energy vs. the amount of component J, with pressure, temperature, and the amounts of the other components held constant (see Fig. 2).
It may be shown that the total Gibbs free energy of a mixture of k components is given by:
where mA , mB , etc. are the chemical potentials at the composition of the mixture, whilst nA, nA, etc. are the number of moles of component A, B, etc. in the mixture (the composition). This means that G is dependent on the composition of the system.
This suggests that our fundamental equation of thermodynamics stating how G changes with T and p need to be updated to include this variation with composition. This new updated equation is given by:
and is now called the fundamental equation of chemical thermodynamics.
At constant temperature and pressure, the fundamental equation of chemical thermodynamics reduces to:
NOTE: The conditions of constant temperature and pressure are the same that make dG equal to the maximum non-expansion work, i.e.: