Dr. Joseph N. Grima, Department of Chemistry
University of Malta, Msida, MSD 06, MALTA
http://staff.um.edu.mt/jgri1/teaching/ch237

We may assume that the energy of a molecule is the sum from contributions from the different modes of motion, namely translation, rotation, vibration and electronic contribution, i.e.: 

This means that we may write the partition function as:

i.e. we may first calculate the partition function for the four contributions separately, and then obtain the molecular partition function as the product of the four. 
 

(3-1) The translational contribution

In classical mechanics, the translational kinetic energy of a particle can assume any value (continuos function). However, at the atomic level, this assumption cannot be made, and instead we have to make use of quantum mechanics, and place limits on the actual kinetic energy that a molecule can have. In particular, if we wish to find what sort of translational energy values a molecule can have, we assume that our molecule is in a box of dimensions X, Y, Z. In such cases, the permitted energy levels e_x for translational motion in the x-direction of a molecule of mass m is constrained by two infinite boundary potentials at x = 0 and x = X, and is given by: 

Thus, since in this case, g(n) = 1, we have:
 

In most normal circumstances, the value of X is so large that these energy levels are close to each other hence forming a so called 'virtual continuum'. This means that we may replace the summation (since q is quantized) by a integral (because of the 'virtual continuum' approximation) to obtain:

which is usually written in the form:

(i) q^trans approaches infinity as T approaches infinity since a large number of states becomes available at very high T. q^transis 0 at 0K.

(ii) Typical values q^trans at room temperature: 2 x 10²⁸ for O₂ in a 100cc vessel.

(iii) Approximations made remain valid if L >> V. For example, for H₂ at 25^oc, L = 0.71Å, which is comparable to the pores in zeolites (5 Å). 
 

(3-2) The rotational contribution

As in the case of translational motion, the rotational motion of a molecule is also quantized. In our discussion of rotational energy, we need to initially suppose that our molecules are rigid rotors, that is bodies that do not deform under the stress of rotation. Rigid rotors may be classified into four types, according to their symmetry/moments of inertia (about three orthogonal axis):
 

(i) spherical rotors, (molecules that belong to cubic or icosahedral groups, e.g. CH₄, SiH4 and SF₆) have three equal moments of inertia

(ii) symmetric rotors, (molecules that have at least a threefold axis of symmetry, e.g. NH₃, C₆H₆, CH₃Cl₄) have two equal moments of inertia, and the third one (the one about the axis of rotational symmetry) being different

(iii) linear rotors, (molecules whose atoms lie in a line, e.g. CO₂, HCl_, OCS, ethyne) have one moment of inertia (the one about the axis) equal to zero, and the two others being equal. 

(iv) asymmetric rotors, (molecules without even a threefold axis of symmetry, e.g. H₂O, H₂CO, CH₃OH) have three different moments of inertia.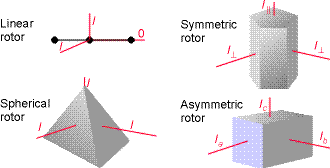 

Fig. A schematic illustration of the classification of rigid rotors.

The derivation of the molecular partition funtion will involve three distinct parts:

(A) Finding the allowed energies for the different rotors
(B) Finding the levels of degeneracy
(C) Computation of  partition function from the energy levels and their degeracy

(A) Let us first have a look at the allowed energies of rotors
 

In classical mechanics, the energy for a rigid body rotating about an axis a is given by:

where w_a is the angular velocity about the a-axis (units: rad s^-1) , and I_a is the moment of inertia about the same axis. Thus for a rigid body free to rotate about the three ortho-axis, we have:

or in terms of the angular momentum J_a about the a-axis (J_a = I_a w_a), we have:

Although in most everyday scenarios E^rot and J_a can take any value (classical mechanics / continuum), at the atomic level, this assumption cannot be made, and instead we have to make use of quantum mechanics, and place limits on the actual values of rotational kinetic energy and angular momenta a molecule can have. 

In particular:

(i) The magnitude of the angular momentum is only allowed to have values of:

where J is the 'angular momentum quantum number' and may have values J = (0,1,2,…)

(ii) The component of the angular momentum about any arbitrary axis (say the z-axis) is only allowed to have values:

where K = J, (J-1), …,1,0, -1, …, -J. 

This means that for example, a symmetric rotor for which is only allowed energies given by:

we thus have:

which may be expressed in terms of parameters A and B (usually listed in data books)as:

were:

and:

The energies for the other types of rotors may be calculated in the same way. For example, in the simpler case of a linear rotor (non-symmetric), where I_a = 0, and for a spherical rotor the energies are given by:

The equivalent expression for the asymmetric rotor is difficult to deduce and shall not be considered. Note also that not all energy levels could be accessible (e.g. homonuclear diatomic molecules such as N₂, H₂, O₂, etc. can only occupy all-even or all-odd J's).

(B) Let us now consider the level of degeneracy (g) for this mode of deformation.

In the case of a the symmetric rotor, we have:

(i) The allowed energies for a symmetric motor is dependent o the values of J and K. In particular, for K ¹ 0, each level is doubly degenerate since:
 



J = 0 , 1, … and K = -J, …, 0, …, J

we have:



(ii) The angular momentum of a molecule has a component on an external, laboratory-fixed axis. This component is also quantized and has values of:



hence giving rise to an additional (2J+1)-fold degeneracy. 


Consequently, all symmetric rotors are:

(i) K ¹ 0, the energy levels are 2(2J+1)-fold degenerate;
(ii) K = 0, the energy levels are (2J+1)-fold degenerate.

• A linear rotor has K fixed at 0. And hence, in this case, we only have a (2J+1)-fold degeneracy.

 
• In the case of a the Spherical rotor, we have:

 

(i) The allowed energies for a symmetric motor (A=B) is dependent on the value of J but not of K However, the quantum number K may still take any of its 2J+1 values. This introduces a (2J+1)-fold degeneracy arising from the orientation in space relative to an arbitrary internal axis.

(ii) As in the case of the symmetric rotor, angular momentum of a molecule has a component on an external, laboratory-fixed axis. This component is also quantized and has values of:



which give rise to an additional (2J+1)-fold degeneracy. Consequently, all spherical rotors have a total of (2J+1)²-fold degeneracy. 

(C) Computation of  partition function from the energy levels and their degeracy
 

Given this information of the energy levels and levels of degeneracy, we should now be in a position to compute the partition function, i.e.:

For example, let us consider the case of a linear non-symmetric rotor, where:

and

In this case, the lower rotational energy level (J=0) is 0, and hence e_J = E.

Thus we have: 

which is usually evaluated numerically for experimental values of the rotational energy levels (measured spectroscopically).

However, although the energy separation between adjacent rotational energy levels is many times larger that that of the translational energy levels, in most cases, this gap is still very small when compared with thermal energy (= kT), and hence we once again may assume a continuum. This means that we may replace the summation (discrete) by an integral.

Thus, for a linear non-symmetric rotor we have:

whilst for non-linear non-symmetric rotors (including the asymmetric rotor), we have:

where A, B, C are rotational constants of the molecules. 

The exceptions when the continuum approximation cannot be made lies for (i) very small molecules (very large gaps), or (ii) for very low temperatures (very low kT), when kT and the gaps in between the rotational energy levels can become comparable. In view of this we make use of the characteristic rotational temperature, q_R, which give us an indication of the possible errors involved when we replace summations by integrals (e.g. T/q_R = 10 => 0.5% error, T/q_R = 1 => 15% error). This characteristic rotational temperature, q_R, is given by:

Typical values of high q_R include H₂ (q_R = 88K), whilst normal ones are for example, 9.4K (HCl), 0.053 (I₂) and 0.561 (CO₂).

Note also, that as we said above, we must make sure not to overestimate the number of rotational states. In particular, homonuclear diatomic molecules and symmetric linear molecules (e.g. CO₂ or ethyne), then rotations through 180^o degrees result in an indistinguishable state of the molecule. Hence the number of thermally accessible states is only half that of non-symmetric species, and hence we have to introduce a symmetry number, s, i.e.:

where s = 1 for non-symmetric linear molecules, and s = 2 for symmetric ones. More formally, s is the order (i.e. the number of elements) of the rotational subgroup of a molecule, i.e. the point group with all but the identity and the rotations removed. 

The same can be applied for other types of symmetries in non-linear molecules, i.e. we get:

Thus, for example, s(H₂O) = 1x2 = 2 reflects the fact that a 360^o/2 rotation about the 1 C₂ axis interchanges two indistinguishable atoms , s(NH₃) = 1x3 = 3 (we have a 360^o/3 rotation about the 1 C₃ axis) and for methane we have s(NH₃) = 4x3 = 12 (we have a 360^o/3 rotation about its four C-H bonds). 

(3-3) The vibrational contribution

We shall commence our discussion of discussion of vibrational terms by considering a diatomic molecule and model this using the classical ball and spring model, where the two atoms (the balls) have masses m₁ and m₂ respectively and are connected by a spring of force constant k₁₂. In such case, the classical vibrational frequency (simple harmonic oscillator) is given by:

v = 0, 1, 2, …

Vibrational energy levels for diatomic molecules are always non-degenerate (this is not the case in the general case of polyatomic molecules).

Polyatomic molecules can undergo may independent vibrational motions. Normal mode analysis (i.e. assuming that an independent, synchronous motion of atoms or groups of atoms within a molecule may be excited without leading to the excitation of any other normal mode) allows us to assume that each normal mode behaves as an independent simple harmonic oscillator. 

In general, a polyatomic molecule of N atoms has 3N degrees of freedom, three of which are assigned to translation of the molecule as a whole, and another 3 (or 2 if molecule is linear) to rotation. This means that a polyatomic molecule of N atoms has (i) 3N-6 normal modes of vibration if it is non-linear, and (ii) 3N-5 normal modes of vibration if it is linear.

Let us now turn our attention to the vibrational partition function. Because we now have 3N-6 (or 3N-5 for linear molecules) normal modes of vibration, our partition function must be a product of the 3N-6 (or 3N-5 for linear molecules) vibrational partition function of the individual modes, i.e.:

Since we are assuming that e₀ = 0, then we have e₁ = h n_(n), e₂ = 2hn_(n), e₃ = 3hn_(n), etc. Thus we have:

Note that when q_V is much larger than the temperature T, then the vibrational partition function will be close to 1, as usually the case (i.e. usually, the molecules are in their ground state w.r.t. rotations. Typically, q_V is ~3000K, i.e. q_V/T is ~10, which gives q^vib = 1/(1-e^-10) »1.) This is in sharp contrast with q^trans »10³⁰ and q^rot »10.

Also, when the bonds are so weak that hn << kT (i.e. |-bhn|<1) or at high temperatures, we may expand the exponential term using the expansion:

(3-4) The electronic contribution

Bu the 'electronic contribution' we are referring to the scenario when an electron moves from one orbital to another. However, the separations of the energy levels are usually too big to be overcome simply by thermal excitation. However, there are some exceptions to this statement, namely:

(a) In some cases, we have n-fold degenerate ground sates (e.g. the alkali metals, have a 2-fold degenerate ground state, corresponding to two orientation of the electronic spin). In such cases, the partition function is equal to the degree of degeneracy, i.e.:

Typical values are: (i) at T = 0, q^elec = 2, since only the doubly degenerate ground state is thermally available, (ii) at high T, q^elec approaches 4, since all the four states become thermally available, and, (iii) at 25^oc, q^elec = 3.1

(3-5) The overall partition function

Given the four contributions to the partition function, we may now compute the overall molecular partition function as the product of the four contributing partition functions, i.e.:

(1) We have assumed that the rotational energy levels are close to each other.

(2) We assumed that the vibrational levels are harmonic.

Such approximations and errors can be avoided by using energy levels that are determined spectroscopically, and then evaluate the sums explicitly.