ST_gasses

CH237 - Chemical Thermodynamics and Kinetics

Dr. Joseph N. Grima, Department of Chemistry
University of Malta, Msida, MSD 06, MALTA
http://staff.um.edu.mt/jgri1/teaching/ch237

BACK TO TABLE OF CONTENTS

Statistical Thermodynamics (v)

Applications of Statistical thermodynamics to perfect gasses.

(1) Derivation of the equation of state of gas of independent particles from statistical thermodynamics
(2) Derivation of the other thermodynamic properties for monoatomic perfect gasses.
(2-1) The Internal energy
(2-2) The enthalpy
(2-3) The entropy and Helmholtz free energy
(2-4) The Gibbs free energy
(2-5) The heat capacities.

[ TOP ]

Applications of Statistical thermodynamics to perfect gasses.

(1) Derivation of the equation of state of gas of independent particles from statistical thermodynamics

We have already said that the pressure of is related to the Canonical partition function by:

However, for independent particles:

i.e.:

Also,

i.e.:

Thus, we may re-write the pressure as: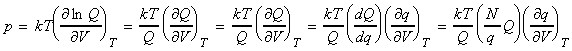

i.e.:

But the pressure of a gas is only effected by the translational motion of gas, and hence, the molecular partition that we would have to use to derive the pressure of a gas is:

where L is the thermal wavelength of the gas particles. Thus, since:

the pressure p is given by:

But, the Boltzmann's constant k is given by:

whilst:

Thus, we have:

i.e. the equation of state of a gas of independent particles is the perfect gas law:

[ TOP ]

(2) Derivation of the other thermodynamic properties for monoatomic perfect gasses.

(2-1) The Internal energy

We have already seen that for a system of independent particles, the internal energy is given by:

and for a monatomic gas, the partition function is the one for translational motion, i.e.:

where L is the thermal wavelength of the gas particles which is given by:

Thus, we have:

But:

i.e.:

Thus we have:

NOTE: For diatomic and polyatomic gasses, we would also need to include the other modes.

[ TOP ]

(2-2) The enthalpy

Since the enthalpy H is related to the internal energy through:

then:

But at T = 0, H(0) = U(0)

[ TOP ]

(2-3) The entropy and Helmholtz free energy

The entropy may be obtained from:

Thus for a monoatomic gas we get:

where q is given by V / L³

Similarly for the Helmholtz free energy:

This equations apply to any state of matter.

[ TOP ]

(2-4) The Gibbs free energy

Unlike the Helmholtz free energy, the Gibbs free energy, G for an ideal monoatomic gas assumes a very simple form since:

i.e.:

which at T=0 gives G(0) = A(0), i.e.:

At this point, the molar partition function may be defined as:

i.e.:

Note that these equations for the Gibbs free energy are valid for any type of ideal gas (monoatomic / diatomic / polyatomic) since they only involve the pV = nRT equation and the equation Helmholtz free energy, which is valid for all states.

[ TOP ]

(2-5) The heat capacities.

The heat capacities for a monoatomic gas may be derived from U and H since for 1 mole of gas:

and:

[ TOP ]

BACK TO TABLE OF CONTENTS

[ UNIVERSITY OF MALTA | FACULTY OF SCIENCE | DEPARTMENT OF CHEMISTRY ]

E-mail me at jgri1@um.edu.mt

http://staff.um.edu.mt/jgri1