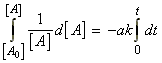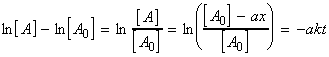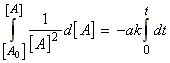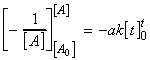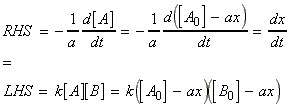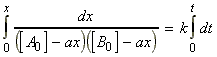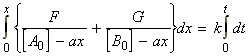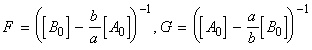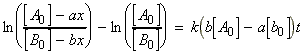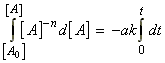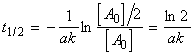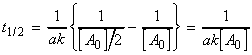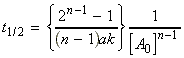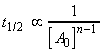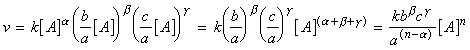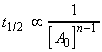Dr. Joseph N. Grima, Department of Chemistry
University of Malta, Msida, MSD 06, MALTA
http://staff.um.edu.mt/jgri1/teaching/ch237

(1-1) The determination of the rate law from:

(a) the isolation method 
(b) method of initial rates 
(c) the integration method 
(d) fractional lifetime method 

(1-1-a) The isolation method 
 

The easiest method to determine a rate law is by the isolation method where the concentrations of all the reactants except one is in large excess. Thus for example, if for the reaction:

which has a rate law of the form:

we let B and C to be in large excess with concentrations [B_o] and [C_o], then it may be assumed that their concentration is constant throughout the reaction. Thus we may write:

where:

This means that if we take logs of both sides we get: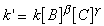

which is the equation of a straight line: 

for plotting ln(v) against ln[A] with gradient a and y-intercept of ln(k`). 

Note that:

Under these conditions, we may say that the reaction has a pseudo -order rather than the true-order.

The process can be repeated by letting A/C and then A/B be in excess to determine a, b, g, and k.

(1-1-b) Method of initial rates
 

In the method of initial rates, the rate is measured at the beginning of the reaction for several different initial concentration of the reactants. Thus for example, for the reaction:

which has a rate law of the form:

or in the limit of t = 0, we get:

where [A₀], [B₀] and [C₀] are the initial concentrations of A, B, C respectively.

In practice, this equation can used if we run a series of experiments to determine v₀ for various initial concentrations of one of the reactions (say A) whilst keeping the concentration of all other reactants (B and C) constant. We may then write:

where:

This means that if we take logs of both sides we get:

which is the equation of a straight line: 

Note: 

The process can be repeated to determine all of a, b, g, and k by running other sets of experiments for various initial concentrations of B, and then C. 

The method of initial rates is often used in conjunction with the isolation method. 

(1-1-c) The integration method 

 
Rate laws are differential equations. Integration of these equations gives us an expression for the concentration of particular species as a function of time. For simple reactions, this integration can be done analytically, and the results from such integrations are summarised in Table  1.

Table 1: Click here for a larger image.
 

In this section we shall illustrate how this process works for four types of rate laws:
 

i.e.:

which integrates to:

This result is usually expressed in terms of the extent of reaction:
 

time	Extent of reaction	[A]
0	0	[A0]
t	x	[A] = [A0] - ax

i.e.:

or in exponential form, i.e.:

Note: Fig. 1 shows how the exponential decay of the reactant in a first-order reaction. The larger the rate constant, the more rapid the decay: here k(large)= 3.k(small).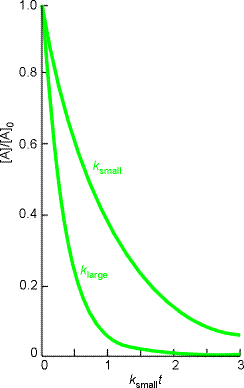

Fig. 1: The exponential decay of the reactant in a first-order reaction

In this case we have:

which integrates to:

i.e.:

   (iii) a second order rate law: 

for the chemical reaction:

In this case we write:
 

time	Extent of reaction	[A]	[B]
0	0	[A0]	[B0]
t	x	[A0] - ax	[B0] - ax

i.e.:

i.e.:

i.e.:

where:

i.e. by integration:

In this case we have:

which integrates to:

i.e.: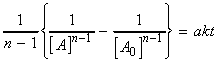

 

(1-1-d) Fractional lifetime method 
 

The half life ( t_1/2) of a reaction  is the time taken for the initial concentrations [A₀], [B₀], … of the reactants to decrease by half.

This means that for example, 

(i) For a first order rate law, where , we have: 

(ii) For a second order rate law where , i.e. , we have:

(iii) For an n^th order rate law where, i.e.: 

, 

we have:

i.e.:

The half lives for a few other rate-laws are given in Table  1. Other fractional life-times may be similarly defined. 
 

Table 1: Click here for a larger image.

Note that for any reaction , starting with a stoichiometric mixture of reactants, we may write:

and hence a rate law of the from:

may be re-written in terms of [A] as:

Thus, for a reaction whose rate is only dependent on the concentration of one reactant, or for stoichiometric mixtures, we have:

i.e.:

(1-2) Comparison of the methods for determining the rate law

Of the four methods discussed above, the integration method is the one most widely employed for evaluating empirical rate laws for which an order of reaction can be defined. However, it has a number of disadvantages:

• Usually only integral or very simple fractional orders are used and a reasonable fit accepted although a better fit with some other non-integral order might be possible. 
• The integration method characterises the way in which the rate varies with time. In certain cases the order with respect to time is different from that found using the initial rate method which gives theorder with respect to concentration.
• If the order as a function of time is larger than the order with respect to concentration this means that, as the reaction proceeds, the rate is decreasing more rapidly than expected from initial rate measurements. This must be due to products which have an inhibiting effect. 
• When the order as a function of time is smaller then the order with respect to concentration, the reverse holds, i.e. the product accelerates the reaction and an autocatalytic reaction is occurring. 

Given this information, one must appreciate that to obtain a full understanding of the rate behaviour initially and throughout a reaction, it is essential to use both initial rate and integration methods to characterise fully the kinetic behaviour of any reaction Systematic studies varying the concentration of each reactant, product and any possible inhibitor or catalyst have to be made, and the resulting kinetic behaviour analysed This is especially true when the rate law does not have a form which allows the assignment of an order of reaction.

See Also: Table 1: Click here - opens in a blank page.