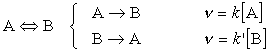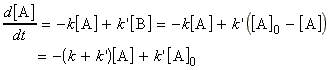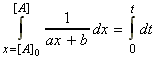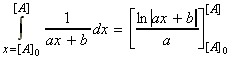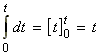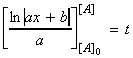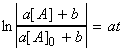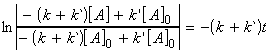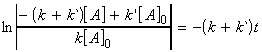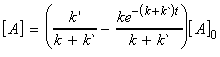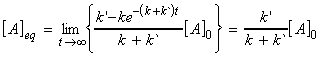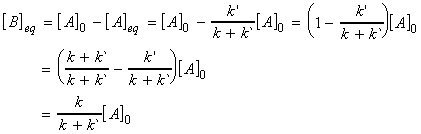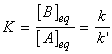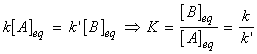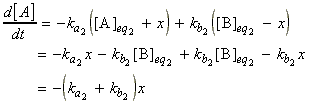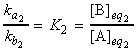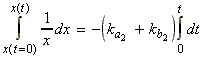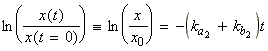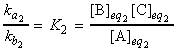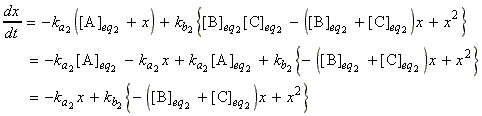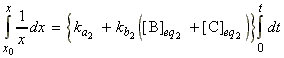7. Empirical Reaction Kinetics (ii)
(1-3) Reactions approaching equilibrium
(1-4) Relaxation techniques
(1-3) Reactions approaching equilibrium
Reactions approaching equilibrium have to be treated in a special way to account for the fact that in proximity to equilibrium conditions, the reverse reaction becomes important.
Let us consider a first order reaction close to equilibrium:
The concentration of A is:
- Reduced by the forward reaction
- Increased by the reverse reaction
But if we let the initial concentration of A be [A]0 then, at all times:
Thus we may from a differential equation:
i.e.:
which is a differential equation of the form:
i.e.:
where:
and:
i.e.:
i.e.:
i.e.:
i.e.:
or:
i.e.:
i.e.:
i.e.:
i.e.:
i.e.:
i.e.:
i.e.:
i.e.:
At t approaches infinity, the concentration of A approach
its equilibrium values, i.e.:
since:
The concentration of B at equilibrium is given by:
and hence the equilibrium constant is given by:
NOTES:
(1) Exactly the same conclusion can be reached (and far more quickly) by noting that at equilibrium, the forward and reverse rates must be equal, i.e.:(2) This equation is a particularly significant as it relates a thermodynamic property (the equilibrium constant) to quantities relating to rates.(3) The practical importance of this equation is that if one of the rate constants is known, the other may be obtained if the equilibrium constant is known.
(4) For a more general reaction, the overall equilibrium constant can be expresses in terms of the rate constants of all the intermediate stages of the reaction mechanism:
where the k s are the rate constants for the individual steps, and the k` s are the rate constants for the corresponding reverse steps.
The term relaxation denotes the return of a system to equilibrium, and in chemical kinetics, it is used to indicate the re-adjusting that a reaction has to make in response to a sudden (normally) disturbance of an equilibrium.
Sudden changes could include:
- A sudden temperature jump (see fig. 1), induced, for example by discharging a cpacitor through a sample made conducting by addition of ions, or, by laser or microwave discharge. Tempertaure chages of 5-10K can be achieved in as little as 1 ms.
- A sudden pressure jump (in cases where the equilibrium is effected by pressure).
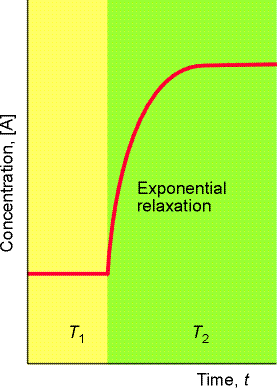
Let us consider the scenario of a sudden temperature increase applied to the equilibrium A B (see Fig. 1).
Let ka1 and kb1 be the rate constants at the initial temperatures T1, that is, prior to the temperature jump, the net rate if change of [A] is given by:
which under equilibrium conditions:
i.e.:
Now let ka2 and kb2 be the rate constants at the final temperatures T2, that is, after to the temperature jump. As before, once we reach the new equilibrium at temperature T2 we have:
Note that this state of equilibrium is reached at a rate that depends that depends solely on the new rate constants ka2 and kb2, that is from:
| At equilibrium with temp. T1 | Instant of change from T1 to T2 | Relaxation | At equilibrium with temp. T2 | |
|
|
|
|
|
|
|
|
|
|
|
|
we obtain (for x in the region between 0 and '[A]eq1 - [A]eq2'):
since:
Also, since [A] = [A]eq2 + x, then: d[A] = dx, i.e.:
Thus we have:
i.e.:
which becomes:
i.e. by raising to the power of e:
or:
where t is known as the relaxation time given by:
Note that through the relaxation time, t, and the new equilibrium constant we may derive ka2and kb2 by simultaneous equations ( K2 = ka2/kb2).
Similar equations may also be derived for other types of elementary reactions.
For example for A B + C where the forward is first order, and the reverse is second order overall, we have:
i.e. at equilibrium 1:
whilst in between equilibrium 1 and 2 we have:
[A] = [A]eq2 + xi.e.:[B] = [B]eq2 - x
[C] = [C]eq2 - x
where:
i.e.:
i.e.:
which since:
we have:
where is we assume that x2 is approximately zero, then:
i.e.:
i.e.:
or:
where:
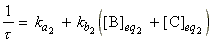
(Exercise - work this in terms of dissociation of water, P.W. Atkins, p. 774, example 25.4)
It can also be shown that for the reaction A + B <=> C
+ D (assuming it is second order in both directions) we have:
where:
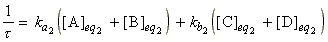
(Exercise - Derive this equation)