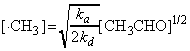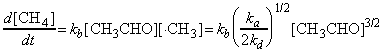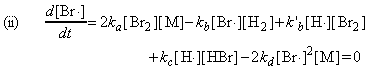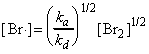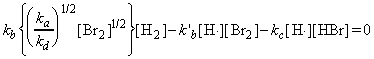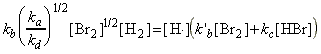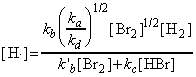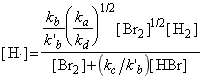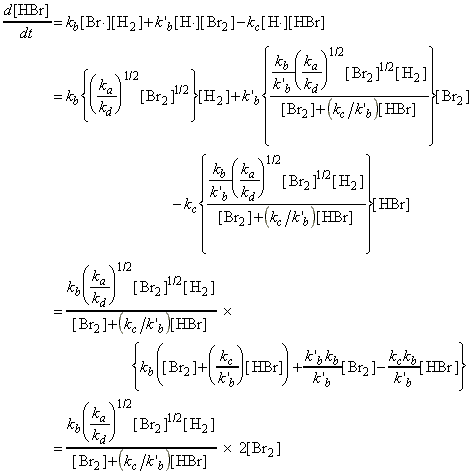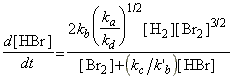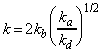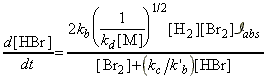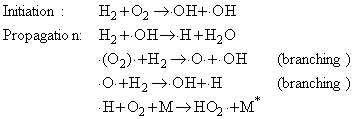(1) Introduction

(2) The rate laws of chain reactions:

(2-1) Example of a chain reaction having a simple rate law - The Rice-Herzfeld mechanism for the pyrolysis of ethanal in the absence of air.

(2-2) Example of a chain reaction having a complicated rate law - The formation of HBr from hydrogen and bromine. (See also this aside.) 

(1) Introduction

A chain reaction is one where an intermediate formed in one step generates an intermediate in a subsequent step, then that intermediate generates another intermediate, and so on. The intermediates in a chain reaction are called chain carriers. In radical chain reactions, radicals (i.e. species with unpaired electrons) act as carriers. Other carriers include neutrons (in nuclear fission) and ions.

Chain reaction involved several types of steps (elementary reactions):

• The initiation step - the step where the chain carriers are initially formed: 
E.g.: Cl atoms are formed by the dissociation of Cl₂ molecules either:
1. through vigorous intermolecular collisions in a thermolysis, i.e. a reaction initiated by heat, or,
2. through absorption of a photon in a photolysis , i.e. a reaction stimulated by the absorption of a electromagnetic radiation.

• Propagation steps - the steps where chain carriers produced in the initiation step attack other reactant molecules, each attach results in the formation of a new carrier. 
E.g.: The attack of a methyl radical on ethane: 
• Branching steps (optional) - steps which result the attach of a chain carrier on a reactant molecule produces more than one chain carrier.
E.g.:
• Retardation steps (optional) - steps in which a chain carrier attack a product molecule formed earlier in the reaction, thus reducing the net rate of product formation. 
E.g.: In the photochemical reaction in which HBr is formed from H₂ and Br₂, we may have  . Note that retardation steps to dot end (terminate) the chain.
• Termination step - a step where carriers combine and end the chain.
E.g.: 
• Inhibition step (optional) - a step where carriers are removed by a process other then termination (i.e. not by having two carriers combining and ending the chain.) Possible ways for inhibition include reaction of the chain carriers with the walls of the reaction vessel or foreign species. 
E.g.: 

(2-1) Example of a chain reaction having a simple rate law - The Rice-Herzfeld mechanism for the pyrolysis of ethanal in the absence of air.

The pyrolysis (i.e. thermal decomposition) of ethanal (acetaldehyde, CH₃CHO) is found to exhibit a simple rate law where:

This reaction proceeds according the Rice-Herzfeld mechanism where:

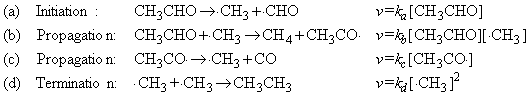
According to steady state approximation, the net rate change of the intermediates may be set to zero, i.e.:

i.e. (i)+(ii) =>

NOTE: Although this mechanism captures the principal features of the reaction, it does not accommodate the formation of various by products such as propanone and propanol. Some of these by-products are formed in significant quantities. All this indicates that the true mechanism for pyrolysis of ethanal must be more complicated than the Rice-Herzfeld mechanism. 

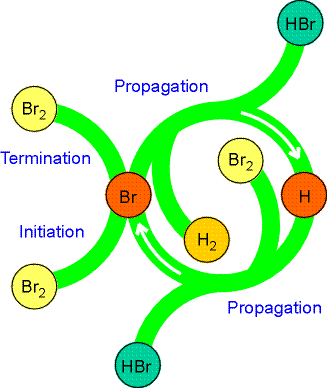
As we had seen in the introductory section of chemical kinetics, although the stoichiometric equation for the reaction between hydrogen and bromine to give HBr looks very simple, the rate law is very complicated indicting a complex mechanism (see fig 1) i.e.:

The proposed mechanism for this reaction (see Fig. 1.) is:

Through this mechanism, it may be deduced that the net rate of formation of HBr (product) is given by:

(1) The presence of [HBr] in the denominator is a sign that HBr is acting as an inhibitor, and reducing the rate of formation of product. Likewise, the presence of [Br₂] stems from the role of Br₂ in the removal of the reactive hydrogen radicals from the chain.

(2) In the examples we have considered, the observed rate laws are reproduced by the mechanisms. In the past, that used to be essentially the end of the calculation (but not of the experimental investigation). However, we can make use of computers to integrate the approximate rate law numerically, and hence predict the time dependence of the HBr concentration. (See Fig. 2). Mathematical software may also be used to integrate the original coupled rate laws without needing to invoke the steady-state approximation.

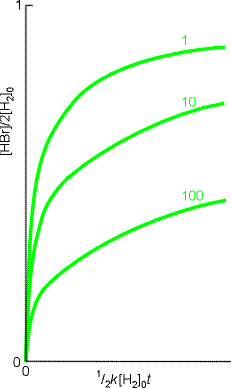
Fig. 2: The numerical integration of the the HBr rate law, can be used to explore how the concentration of HBr changes with time. These runs began with stoichiometric proportions of hydrogen and bromine; the curves are labelled with the value of 2k'-1.

(3) HBr may also be produced through in a process where the initiation step is photochemical. In this case, the initiation step is of the form:

where  represents the rate at which photons of the appropriate frequency are absorbed by the volume in which the reaction occurs. In this case, the rate of formation of HBr in this case is given by:

(a) A thermal explosion is due to the rapid increase of reaction rate with increasing temperature. If the energy released by an exothermic reaction cannot escape, the temperature of the system rises and the reaction goes faster. The acceleration of the rate results in a faster rise of temperature, so the reaction goes even faster... catastrophically fast. 

(b) A chain-branching explosion may occur when there are chain-branching steps in a reaction, for then the number of chain centres grows exponentially and the rate of reaction may cascade into an explosion.

An example of both types of explosion is provided by the reaction between hydrogen and oxygen: 

The two branching steps can lead to a chain-branching explosion. The HO₂^. radicals are eliminated by collisions with the walls. 

The occurrence of an explosion depends on the temperature and pressure of the system, and the explosion regions for the reaction are shown in Fig. 3:

• At very low pressures the system is outside the explosion region and the mixture reacts smoothly. At these pressures the chain carriers produced in the branching steps can reach the walls of the container where they combine. 
• Increasing the pressure (along a vertical line in the illustration) takes the system through the first explosion limit (if the temperature is greater than about 730 K). The mixture then explodes because the chain carriers react before reaching the walls and the branching reactions are explosively efficient. 
• The reaction is smooth when the pressure is above the second explosion limit. The concentration of molecules in the gas is then so great that the radicals produced in the branching reaction combine in the body of the gas, and reactions such as  can occur. Recombination reactions like this one are facilitated by three-body collisions because the third body (M) can remove the excess energy. At low pressures three-particle collisions are unimportant and recombination is much slower. At higher pressures, when three-particle collisions are important, the explosive propagation of the chain by the radicals is partially quenched because the branching steps are diverted into simple propagation steps. 
• When the pressure is increased to above the third explosion limit, the reaction rate increases so much that a thermal explosion occurs. In this limit the reaction:  dominates the elimination of HO₂^. by the walls.

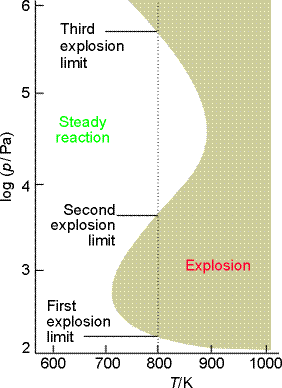
Fig. 3: The explosion limits of the hydrogen + oxygen reaction. In the explosive regions the reaction proceeds explosively when heated homogeneously.