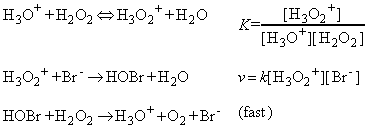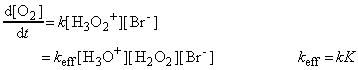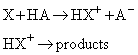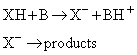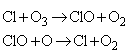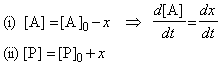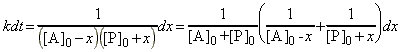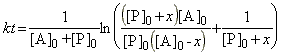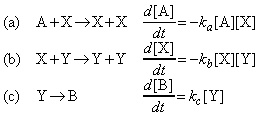(1) Catalysis
(2) Autocatalysis
(3) Oscillating reactions
(1) Catalysis
Def'n: A catalyst is a substance that accelerates a reaction but undergoes no net chemical change. It functions by lowering the activation energy of the reaction by providing an alternative path that avoids the slow, rate-determining step of the uncatalysed reaction, and results in a higher reaction rate at the same temperature. (Note: If the activation energy of a reaction is high, at normal temperatures only a small proportion of molecular encounters result in reaction.)
Def'n: A heterogeneous catalyst is in a different phase (for example, a solid catalyst for a gas-phase reaction).
Def'n: A homogeneous catalyst is a catalyst that is in the same phase as the reaction mixture (for example, an acid added to an aqueous solution). (See below for a discussion).
Catalysts can be very effective; for instance:
- The activation energy for the decomposition of hydrogen peroxide in solution is 76 kJmol-1, and the reaction is slow at room temperature. When a little iodide is added, the activation energy falls to 57 kJmol-1, and the rate constant increases by a factor of 2000.
- Enzymes (biological catalysts), are very specific and can have a dramatic effect on the reaction they control. The activation energy for the acid hydrolysis of sucrose is 107 kJmol-1 but the enzyme saccharase reduces it to 36 kJmol-1, corresponding to an acceleration of the reaction by a factor of 1012 at body temperature (310 K).
(a) The kinetics of the bromide-catalysed decomposition of hydrogen peroxide at low pH:
This reaction is believed to proceed through the following pre-equilibrium:
(NOTE: In the equilibrium constant, the activity of water has been set equal to 1.)
Because the second step is rate-determining, the rate law of the overall reaction is obtained by setting the overall rate equal to the rate of the second step and using the equilibrium constant to express the concentration of H3O2+ in terms of the reactants:
in agreement with the observed dependence of the rate on the Br- concentration and the pH of the solution.
The observed activation energy is that of the effective rate coefficient kK. In the absence of Br- ions the reaction cannot proceed through the path set out above, and a different and much higher activation energy is observed.
(b) Acid catalysis
In acid catalysis, the central step is the transfer of a proton to the substrate:
Examples include the primary process in the solvolysis of esters and keto-enol tautomerism.
(c) Base catalysis
In base catalysis, a hydrogen ion is transferred from the substrate to a base:
It is the primary step in the isomerization and halogenation of organic compounds, and of the Claisen and aldol reactions.
(d) Homogenous catalysis and atmospheric chemistry
Homogeneous catalytic cycles play a role in atmospheric chemistry. For instance, the presence of chlorine atoms resulting from the photolysis of CFCs (chlorofluorocarbons) can participate in the decomposition of ozone in the stratosphere:
The mechanism is illustrated in Fig. 1.
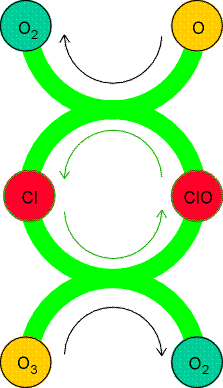
Fig. 1: A catalytic cycle showing the propagation of ozone decomposition by chlorine atoms. Note how the Cl atoms are recycled.
(2) Autocatalysis
The phenomenon of autocatalysis is the catalysis of a reaction by the products. For example, in a reaction A -> P it may be found that the rate law is v=k[A][P] so the reaction rate increases as products are formed.
Such reactions get started because there are usually other reaction routes for the formation of some P initially, which then takes part in the autocatalytic reaction proper.
An example of autocatalysis is provided by two steps in the Belousov-Zhabotinskii reaction where the Product HBrO2 is a reactant in the first step:
The industrial importance of autocatalysis (which occurs in a number of reactions, such as oxidations) is that the rate of the reaction can be maximized by ensuring that the optimum concentrations of reactantandproduct are always present.
Let us now discuss more detail the general autocatalytic reaction named above, i.e.:
We may write:
i.e. the rate law becomes:
i.e. separating the variables we get:
which may be integrated from (t,x)=(0,0) to (t,x) to give:
which may be re-arranged to give:
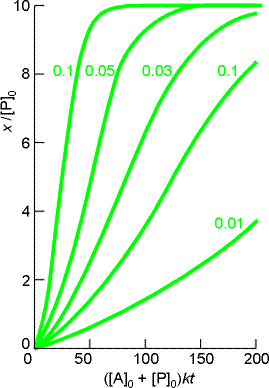
The solution to this equation is plotted in Fig. 2. Note that the rate of reaction is slow initially (when little P is present) and finally slow again (when little A is present - it has all been converted to P !!!)
Fig. 2: The concentration of product during the autocatalysed A -> P reaction. Individual curves are labelled with the value of b.
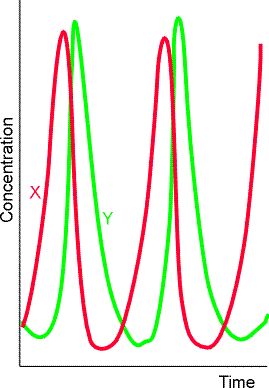
A consequence of autocatalysis is the possibility that the concentrations of reactants, intermediates, and products will vary periodically either in time (see Fig. 3) or even in space (fig. 4). Chemical oscillation is the analogue of electrical oscillation, with autocatalysis playing the role of positive feedback.
Fig. 3: The periodic variation of the concentrations of the intermediates X and Y in a Lotka-Volterra reaction. The system is in a steady state, but not at equilibrium.

Apart from the pure scientific interest associated with these phenomena, oscillating reactions are very frequent in biochemical systems where a cell plays the role of a chemical reactor. Oscillating reactions, for example, maintain the rhythm of the heartbeat. They are also known to occur in the glycolytic cycle, in which one molecule of glucose is used to produce (through enzyme-catalysed reactions involving ATP) two molecules of ATP. The concentrations of all the metabolites in the chain oscillate under some conditions, and do so with the same period but with different phases. There are also some (through very few) oscillating industrial processes.
In this section we shall look at one particular example of an oscillating reaction, namely the Lotka-Volterra mechanism, an autocatalytic reaction of a particularly simple form that illustrates how these oscillations may occur. (Note: The actual chemical examples that have been discovered so far have a different mechanism).
The Lotka-Volterra mechanism is as follows:
where:
- Steps (a) and (b) are autocatalytic.
- The concentration of A is held constant by supplying it to the reaction vessel as needed.
- B plays no part in the reaction once it has been produced, so it is unnecessary to remove it; in practice, though, it would normally be removed.
The Lotka-Volterra equations can be solved numerically, and the results can be depicted in two ways:
- Plot [X] and [Y] against time (Fig. 4);
- Plot one concentration against the other (Fig. 5).

Fig. 5: An alternative representation of the periodic variation of [X] and [Y] is to plot one against the other. Then the system describes closed orbits; different orbits are obtained with different starting conditions.
The periodic variation of the concentrations of the intermediates can be explained as follows:
- At some stage there may be only a little X present, but reaction (a) provides more, and the production of X autocatalyses the production of even more X. There is therefore a surge of X.
- However, as X is formed, reaction (b) can begin. It occurs slowly initially, because [Y] is small, but autocatalysis leads to a surge of Y.
- This surge, though, removes X, and so reaction (a) slows, and less X is produced.
- Because less X is now available, reaction (b) slows.
- As less Y becomes available to remove X, X has a chance to surge forward again, and so on,
1. The reactions must be far from equilibrium.The last criterion is called bistability, and is a property that takes us well beyond what is familiar from the equilibrium properties of systems, and is beyond the scope of this course. (Note: More details are available in your textbook.)2. The reactions must have autocatalytic steps.
3. The system must be able to exist in two steady states.
[ TOP ]