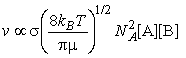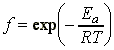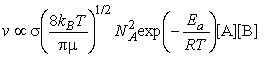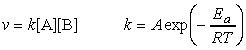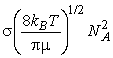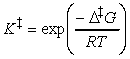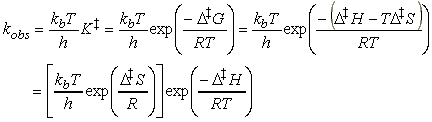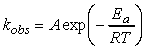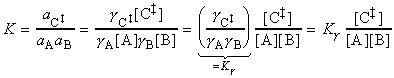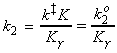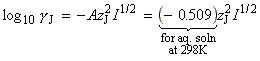A Theoretical approach to reaction
rates:
The Collision theory and the Activated
Complex Theory
In this section we will be deriving from first principles the rate law for the chemical equation A + B -> P, given empirically by v = k[A][B]. This will be done through:
(2) Activated complex theory
(2-1) The reaction profile in the ACT
In this section we shall attempt to understand the origin of the Arrhenius parameters by studying a class of gas-phase reactions in which reaction occurs when two molecules meet (collision theory).
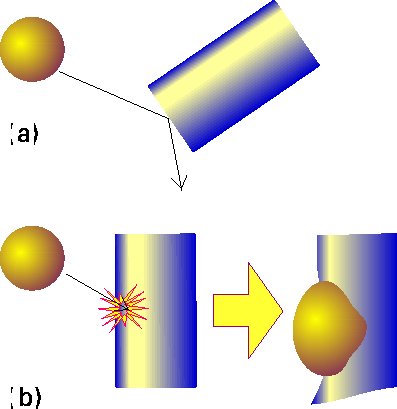
Under this theory, reaction occurs only if two molecules collide with a certain minimum kinetic energy along their line of approach (Fig. 1). In fact, in the collision theory, a reaction resembles the collision of two defective billiard balls: the balls bounce apart if they collide with only a small energy, but might smash each other into fragments (products) if they collide with more than a certain minimum kinetic energy. This model of a reaction is a reasonable first approximation to the types of process that take place in planetary atmospheres and govern their compositions and temperature profiles.
NOTE: The importance of the collision theory is that it provides
a 'proof' from first principles that reactions (or, strictly speaking,
gas phase reactions!) can indeed display Arrhenius-like behaviour.
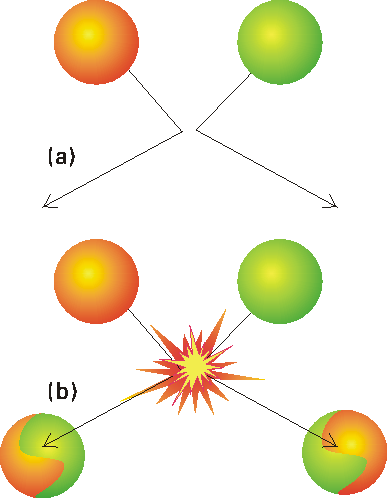
Fig. 1: In the collision theory of gas-phase chemical reactions, reaction occurs when two molecules collide, but only if the collision is sufficiently vigorous, (a) An insufficiently vigorous collision: the reactant molecules collide but bounce apart unchanged, (b) A sufficiently vigorous collision results in a reaction.
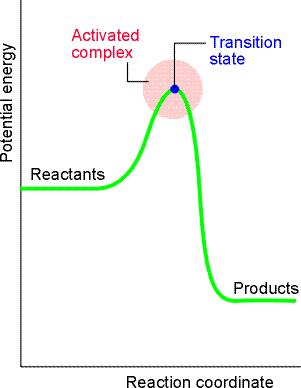
A reaction profile in collision theory is a graph showing the variation
in potential energy as one reactant molecule approaches another and the
products then separate (Fig 2). (NOTE: Recall that the potential energy
of an object is the energy arising from its position (not speed), in this
case the separation of the two reactant molecules as they approach, react,
and then separate as products.)
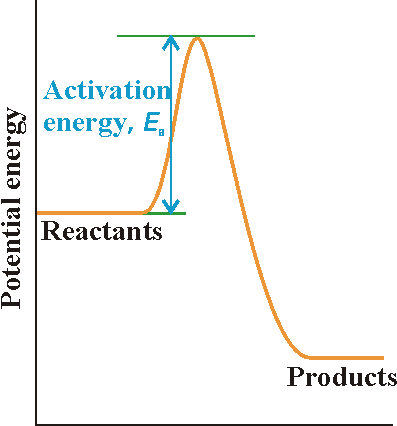
This profile shows:
- On the left, the horizontal line represents the potential energy of the two reactant molecules that are far apart from one another.
- The potential energy rises from this value only when the separation of the molecules is so small that they are in contact, when it rises as bonds bend and start to break.
- The potential energy reaches a peak when the two molecules are highly distorted.
- Then it starts to decrease as new bonds are formed.
- At separations to the right of the maximum, the potential energy rapidly falls to a low value as the product molecules separate.
(1-2) Derivation of the rate law through the Collision theory:
With the reaction profile in mind, the collision theory predics that the rate law for a reaction:
is proportional to:
(a) The encounter rate;where:
(b) The minimum energy requirement;
(c) The steric factor.
(a) The encounter rate:
The rate of collisions between species A and B is proportional to both their concentrations: if the concentration of B is doubled, then the rate at which A molecules collide with B molecules is doubled, and, if the concentration of A is doubled, then the rate at which B molecules collide with A molecules is also doubled. The kinetic theory of gasses goes even a step further and allows us to write:
where NA is Avogadro's constant, kB is Boltzmann's constant, T is the temperature, s is the collision cross-section (see fig. 3), and m is the reduced mass given by:
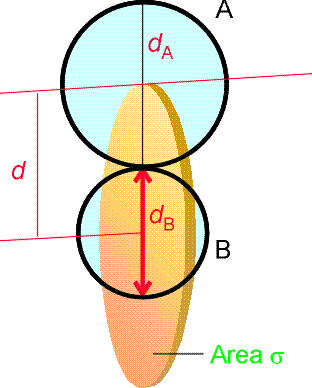
Fig. 3: The collision cross-section for two molecules can be regarded to be the area within which the centre of the projectile molecule (A) must enter around the target molecule (B) in order for a collision to occur. If the diameters of the two molecules are dA and dB, the radius of the target area is d = 1/2 (dA + dB) and the cross-section is pd2.
(b) The minimum energy requirement:
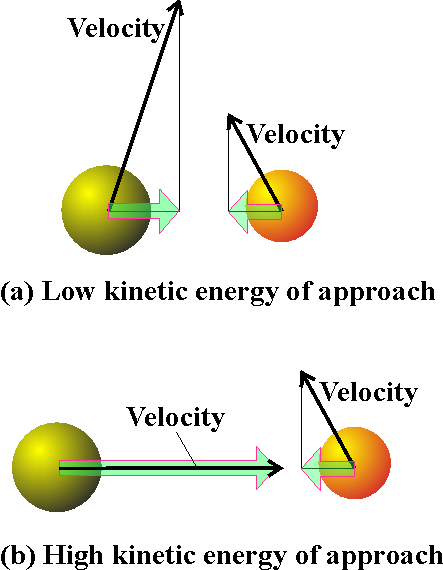
Next, we need to multiply the collision rate by a factor f that represents the fraction of collisions that occur with at least a kinetic energy Ea along the line of approach (Fig 4), for only these collisions will lead to the formation of products. Molecules that approach with less than a kinetic energy Ea will behave like a ball that rolls toward the activation barrier, fails to surmount it, and rolls back.
Fig. 4: The criterion for a successful collision is that the two reactant species should collide with a kinetic energy along their line of approach that exceeds a certain minimum value Ea that is characteristic of the reaction. The two molecules might also have components of velocity (and an associated kinetic energy) in other directions (for example, the two molecules depicted here might be moving up the page as well as towards each other): but only the energy associated with their mutual approach can be used to overcome the activation energy.
It follows from very general arguments concerning the probability that a molecule has a specified energy that the fraction of collisions that occur with at least a kinetic energy Ea is (from the kinetic theory of gasses):
i.e. at this stage we can conclude that the rate of reaction, which is proportional to the rate of collision multiplied by the fraction of successful collisions, is:Note that this equation now has the Arrehenius form, i.e.:This means that at this stage we can already conclude that The activation energy, Ea, is the minimum kinetic energy required for a collision to result in reaction.
(c) The steric factor
However, it is often found that the experimental value of A is smaller than that calculated from the kinetic theory so far, i.e.:
One possible explanation is that, not only must the molecules collide with sufficient kinetic energy, but they must also come together in a specific relative orientation (Fig 5).It follows that the reaction rate is proportional to the probability that the encounter occurs in the correct relative orientation. The pre-exponential factor A should therefore include a steric factor, P, which usually lies between 0 (no relative orientations lead to reaction) and 1 (all relative orientations lead to reaction).
E.g. 1: The reactive collision in which two NOCl molecules collide and break apart into two NO molecules and a Cl2 molecule:
E.g. 2: For the hydrogen addition reaction in which a hydrogen molecule attaches directly to an ethene molecule to form an ethane molecule:This very low value of P which suggests that the reaction has very stringent orientational requirements.Some reactions have P > 1. Such a value may seem absurd, because it appears to suggest that the reaction occurs more often than the molecules meet! An example of a reaction of this kind is the reaction in which a K atom plucks a Br atom out of a Br2 molecule:
In this reaction, the distance of approach at which reaction can occur seems to be considerably larger than the distance needed for deflection of the path of the approaching molecules in a non-reactive collision! To explain this surprising conclusion, it has been proposed that the reaction proceeds by a 'harpoon mechanism'.ASIDE: The harpoon mechanism is based on a model of the reaction that pictures the K atom as approaching the Br2 molecules, and when the two are close enough an electron (the harpoon) flips across to the Br2 molecule. In place of two neutral particles there are now two ions, and so there is a Coulombic attraction between them: this attraction is the line on the harpoon. Under its influence the ions move together (the line is wound in), the reaction takes place, and KBr and Br emerge. The harpoon extends the cross-section for the reactive encounter and we would greatly underestimate the reaction rate if we used for the collision cross-section the value for simple mechanical contact between K and Br2.
(2) Activated complex theory
Fig. 5: Energy is not the only criterion of a successful reactive encounter, for relative orientation may also play a role. (a) In this collision, the reactants approach in an inappropriate relative orientation, and no reaction occurs even though their energy is sufficient, (b) In this encounter, both the energy and the orientation are suitable for reaction.
The activated complex theory (ACT), formerly known as the transition state theory, is a more sophisticated theory of reaction rates that offers the following advantages over the collision theory:
- It can be applied to reactions taking place in solution as well as in the gas phase;
- The advantage that a quantity corresponding to the steric factor appears automatically, in contrast to the collision theory where P had to be grafted on as an afterthought.
(1) The concepts used in the derivation of the rate constants in terms of the ACT are based on statistical thermodynamics.
(2) The reason why P appears automatically in the ACT framework is that the orientation requirements are carried in the entropy of activation. Thus, if there are strict orientation requirements (for example, in the approach of a substrate molecule to an enzyme), then the entropy of activation will be strongly negative (representing a decrease in disorder when the activated complex forms), and the pre-exponential factor will be small. In practice, it is occasionally possible to estimate the sign and magnitude of the entropy of activation and hence to estimate the rate constant.
(3) The general importance of activated complex theory is that it
shows that even a complex series of events (not only a collisional encounter
in the gas phase) displays Arrhenius-like behaviour, and that the concept
of activation energy is applicable.
- Initially, only reactants A and B are present.
- As the reaction event proceeds, A and B come into contact, distort, and begin to exchange or discard atoms.
- The potential energy rises to a maximum and the cluster of atoms that corresponds to the region close to the maximum are referred to the activated complex, (AB)‡ or C‡. The configuration at the actual peak of the potential energy curve is called the transition state.
- After the maximum, the potential energy falls as the atoms rearrange in the cluster, and it reaches a value that is characteristic of the products, P.
Fig. 6: A reaction profile. The horizontal axis is the reaction coordinate, and the vertical axis is potential energy. The activated complex is the region near the potential maximum, and the transition state corresponds to the maximum itself.
In other words we have:
which in terms for the ACT, we have:
or:
i.e. the reaction between A and B proceeding through the formation of an activated complex, C‡, that falls apart by unimolecular decay into products, P. Note that we not all (AB)‡ will proceed to products, and in fact, some will decay back to A and B, i.e.
The scope now becomes to derive an expression for k2 from first principles, which as we have said before, is done through concepts from statistical thermodynamics. This formulation is known as the Eyring equation.
In a simple form of activated complex theory, we suppose that the activated complex is in equilibrium with the reactants (pre-equilibrium), and that we can express its abundance in the reaction mixture in terms of an equilibrium constant, K‡.
Then, if we suppose that the rate at which products are formed is proportional to the concentration of the activated complex, we can write:
The full activated complex theory gives an estimate of the constant of proportionality to give:
Thus, if we compare this expression with the form of the rate law, i.e.:
we would find:
But since we may think of K‡ as an equilibrium constant, then it may be expressed in terms of the standard reaction Gibbs energy, or in this context, the activation Gibbs energy, and written D‡G. It follows that:
i.e.:
But:
i.e.:
This expression has the form of the Arrhenius expression, i.e.:
if we identify the enthalpy of activation, D‡H, with the activation energy and the term in square brackets, which depends on the entropy of activation, D‡S, with the pre-exponential factor.
(2-3) The activated complex theory and reactions between ions.
The simplified (thromodynamic) approach to the activated complex theory simplifies the discussion of reactions in solution. We can combine the rate law:
with the thermodynamic equilibrium constant:
i.e.:
Let us now define ko2 as the rate constant with the activity coefficients equal to 1, i.e.: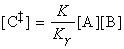
At low concentrations the activity coefficients can be expressed in terms of the ionic strength, I, of the solution by using the Debye-Huckel limiting law (see P.W. Atkins, Physical Chemistry, 6th Ed. Section 10.2c, particularly eqn 10.19) in the form:
where A = 0.509 in aqueous solution at 298 K and zJ is the charge numbers on particle J.
Thus,
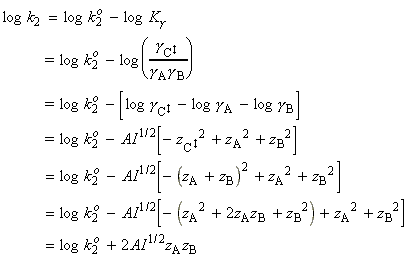 (Eqn. K.Salt.Effect)
(Eqn. K.Salt.Effect)
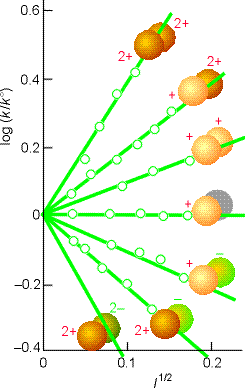
This equation expresses the kinetic salt effect, the variation
of the rate constant of a reaction between ions with the ionic strength
of the solution (see fig. 6):
- If the reactant ions have the same sign (as in a reaction between cations, or, between anions), then increasing the ionic strength by the addition of inert ions increases the rate constant.
- Conversely, ions of opposite charge react more slowly in solutions of high ionic strength.
Conversely, if reactant ions have opposite same signs, the charges in the activated complex cancel out and the complex has a less favourable interaction with its atmosphere than the separated ions with a solution of a high ionic strength.
>> TECHNICAL NOTE: A plot of log(k/k0)
vs. l1/2 should be linear wheer the gradient gtives infomation
about the charge type of the activated complex for the rate determining
step. (see Fig 5 below).
Fig. 6: Experimental tests of the kinetic salt effect for reactions in water at 298 K. The ion types are shown as spheres, and the slopes of the lines are those given by the Debye-Hückel limiting law and the Kinetic salt effect equation above (Eqn. K.Salt.Effect).