 |
CH237 - Chemical Thermodynamics
and Kinetics
Dr.
Joseph N. Grima, Department
of Chemistry
|
 |
CH237 - Chemical Thermodynamics
and Kinetics
Dr.
Joseph N. Grima, Department
of Chemistry
|
|
Aside: The Kinetic Theory of Gasses (1-0) Aside - The kinetic theory of gasses (1-0-0) Introduction [ TOP ]
(1-0-0) Introduction The kinetic model of gases is based on three assumptions:
[ TOP ]
(1-0-1) Molecular speeds
In a time interval Dt we have many molecules colliding with a particular wall. Thus the change in momentum in a Dt time interval is given by: Total momentum change = D momentum for 1 molecule x no. of colliding molecules where:
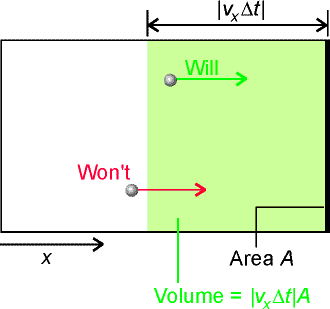

and hence the pressure on this wall is given by: Also, because the molecules re moving randomly, then we may assume that:
i.e.: Also since pV = nRT then we have: i.e.: Note that this expression is for the root mean square speed (which is not the mean speed) of molecules, and, in reality:
where: This expression for f(v) is known as the Maxwell distribution of speeds, sketches of which are given in the figure 3 below.
Fig. 3: The distribution of molecular speeds with temperature and molar mass. Note that the most probable speed (corresponding to the peak of the distribution) increases with temperature and with decreasing molar mass and, simultaneously, the distribution becomes broader.
i.e.: It may also be shown that the most probably speed, c* is given by: whilst the relative mean speed of similar/dissimilar molecules, that is, the mean speed with which one molecule approaches another is: 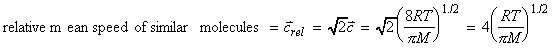 
where m is the reduced mass of the molecules that relates to the individual masses of two dissimilar molecules (mA and mB) though: Note that when mA = mBthen these two expressions become equivalent, since: i.e.:
[ TOP ]
(1-0-2) The collision frequency and mean free path
Let us now calculate the frequency with which molecular collisions occur and the distance a molecule travels on average between collisions for a single-species gas. We count a 'hit' whenever the centres of two molecules come within a distance d of each other, where d, the collision diameter, is of the order of the actual diameters of the molecules (for impenetrable hard spheres d is the diameter) (see fig. 4). Let us assume that the positions of all the molecules except one to
be frozen. When one mobile molecule travels through the gas with a mean
relative speed for a time Dt, it sweeps
out a 'collision tube' of cross-sectional area s
= p d2 and length where where NA is Avogadro's constant. The number of hits scored in the interval Dt is equal to this number, so the number of collisions divided by the time interval, or, the collision frequency, z, is given by: The area s = pd2 is known as the collision cross-section. Given this expression for the collision frequency, z, it may be deduced that the mean time between collisions is 1/z, i.e. the average distance traveled between collisions, or, the mean free path, l, is given by: We an write the collision frequency and the mean free path in terms of pressure by: and: i.e. the collision frequency increases with increasing temperature in a sample held at constant volume. The reason is that the mean relative speed increases with temperature. At constant temperature, the collision frequency is proportional to the pressure. Such a proportionality is plausible for, the greater the pressure, the greater the number density of molecules in the sample, and the rate at which they encounter one another is greater even though their average speed remains the same. Doubling the pressure reduces the mean free path by half. A typical mean free path for nitrogen gas at 1 atm is 70 nm, or about 103 molecular diameters. Although temperature appears in the equation for the mean free path, in a sample of constant volume, the pressure is proportional to T, so T/p remains constant when the temperature is increased. Therefore, the mean path is independent of the temperature in a sample of gas in a container of fixed volume The distance between collisions is determined by the number of molecules present in a given volume, not by the speed at which they travel. Thus to summarise, a typical gas (nitrogen or oxygen) at 1 atm and
25 °C can be thought of as a collection of molecules traveling with
a mean speed of about 350 ms-1. Each molecule makes a collision
within about 1 ms, and between collisions it
travels about 102 to 103 molecular diameters. The kinetic model of gases
is valid (and the gas behaves nearly perfectly) if the diameter of the
molecules is much smaller than the mean free path, for then the molecules
spend most of their time far from one another and do not interact.
|
| E-mail me at jgri1@um.edu.mt |