 |
CH237 - Chemical Thermodynamics
and Kinetics
Dr.
Joseph N. Grima, Department
of Chemistry
|
 |
CH237 - Chemical Thermodynamics
and Kinetics
Dr.
Joseph N. Grima, Department
of Chemistry
|
|
A theoretical investigation of chemical kinetics - Derivation of the rate constant from first principles (iii) (2) Activated complex theory (2-0) Introduction [ TOP ]
(2) Activated complex theory
The activated complex theory (ACT) or the transition state theory, as it is sometimes aclled, is a theory where rate constants are calculated using concepts from statistical thermodynamics. It has the advantage that a quantity corresponding to the steric factor appears automatically, in contrast to the collision theory where P had to be grafted on as an afterthought. Activated complex theory is an attempt to identify the principal features governing the magnitude of a rate constant in terms of a model of the events that take place during the reaction. Let us have a look at a typical the reaction profile (i.e.a plot of the 'potential energy' vs. 'reaction coordinate'), for a bimolecular reaction between A and B forming products P (fig. 1). This plot illustartes the following features:
Fig. 1: A reaction profile. The horizontal axis is the reaction coordinate, and the vertical axis is potential energy. The activated complex is the region near the potential maximum, and the transition state corresponds to the maximum itself. In other words we have: which in terms for the ACT, we have: or: i.e. the reaction between A and B proceeding through the formation of an activated complex, C‡, that falls apart by unimolecular decay into products, P. Note that we not all (AB)‡ will proceed to products, and in fact, some will decay back to A and B, i.e. The scope now becomes to derive an expression for k2 from first principles, which as we have said before, is done through concepts from statistical thermodynamics. This formulation is known as the Eyring equation.
[ TOP ]
(2-1) The Eyring equation
From the discussion above, the rate of reaction, that is the rate of production of P is given by: where the concentration of the activated complex [C‡] is assumed to be proportional to the concentrations of A and B, i.e.: i.e.: Thus the task reduces to finding:
[ TOP ]
(2-1-1) The rate of decay of the activated complex
The rate of decay of the activated complex can be derived through the following observations:
where k is the transmission coefficient. In the absence of information to the contrary, k is assumed to be about 1.
[ TOP ]
(2-1-2) The concentration of the activated complex
The simplest procedure for estimating the concentration of the activated complex in terms of the concentrations of A and B is to assume that there is a pre-equilibrium between the reactants and the complex, and hence write: where pJ is the partial pressure of J which can be expressed in terms of [J], the concentration of J, as follows: i.e.: i.e.: where K is the equilibrium constant. But we have already seen that K can be obtained in terms standard molar partition functions, i.e.: where: Note that the units of NA and the qJ are mol-1, so K is dimensionless (as is appropriate for an equilibrium constant). Let us now direct our attention to the partition function of the activated complex. We have already assumed that a vibration of the activated complex C‡ tips it through the transition state. The partition function for this vibration is: where n is its frequency (the same frequency that determines k‡). This frequency is much lower than for an ordinary molecular vibration because the oscillation corresponds to the complex falling apart (see fig. 27.7), so the force constant is very low. Therefore, because hn /kT << 1, the exponential may be expanded and the partition function reduces to: we may hence write: where with 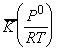 being
a kind of equilibrium constant, but with one vibrational mode of it discarded
(compare it to the general equation for the equilibrium constants in terms
of the partition function). being
a kind of equilibrium constant, but with one vibrational mode of it discarded
(compare it to the general equation for the equilibrium constants in terms
of the partition function).
Fig. 2: In an elementary depiction of the activated complex close to the transition state, there is a broad, shallow dip in the potential energy surface along the reaction coordinate. The complex vibrates harmonically and almost classically in this well.NOTE: There is a real problem here. Figure 2 is probably an oversimplification, for in many cases, there is no dip at the top of thf barrier, and the curvature of the potential energy, and therefore the force constant, is negative. Formally, the vibrational frequency is then imaginary, athough we shall ignore this problem here. [ TOP ]
(2-1-3) The rate constant
Given all this information, we can now combine all the parts of the calculation into one equation, i.e.: i.e. the unknown frequencies n cancels out, and we obtain the famous Eyeing equation: where The rate constant may hence be obtained in terms of the partition functions of A, B, and C‡ by: in accordance with our empirical 'Arrenhius equation': Thus in principle, we now have an explicit expression for calculating the second-order rate constant for a bimolecular reaction in terms of the molecular parameters for the reactants and the activated complex, and the quantity k . The partition functions for the reactants can normally be calculated quite readily, using either spectroscopic information about their energy levels or the approximate expressions taken from the literature. The difficulty with the Eyring equation, however, lies in the calculation of the partition function of the activated complex: C‡ cannot normally be investigated spectroscopically, and in general we need to make assumptions about the size, shape, structure of the complex. In view of all this, let us now make the approximation that we have two structureless particles, A and B, colliding to form an activated complex that resembles a diatomic molecule. The problem reduces evaluation of the partition function of A, B and C‡ (or rather the 'modified' partition function for C‡, modified to remove the vibrational mode along the reaction coordinate) and substituting these into the Eyring equation above. In all cases, we shall assume that the our particle is in the ground electronic state, which is not degenerate, i.e. q(elec) = 1. This means that we no not need to include it in the calculation. (a) The partition function of the reactants, A, B: The reactants J =A,B are structureless 'atoms', and hence, the only contributions to their partition functions are the translational terms: where: and: i.e.:
The activated complex C‡ may be considered as a diatomic cluster of mass mC = mA + mB and moment of inertia I, which for a 'diatomic molecule' of bond length r is given by I = mr2 where m is the effective mass given by: In general a diatomic molecule will have translational, rotational and vibrational contributions to the partition function, i.e.: However in this case we have to remember that although the activated complex has one vibrational mode (as any other diatomic molecule), this vibrational mode corresponds to motion along the vibrational coordinate. Thus, this mode is NOT included in our 'modified' partition function of C‡ (modified to remove the vibrational mode along the reaction coordinate), i.e.: where: (1) The translational contribution is given by: (2) The rotational contribution is given by:
Given all this information we are now in a position to write down the Eyring equation for a reaction between the two structureless particles A, B:
i.e.:
which simplifies to:
(trust me!)
Thus if we where to identify the reactive cross-section, s* as: we obtain the same result as in the collision theory, i.e.
[ TOP ]
(2-2) The experimental observation of the activated complex Until very recently there were no direct spectroscopic observations on activated complex for they have a very fleeting existence and often survive for only a picosecond or so. However, the development of femtosecond pulsed lasers and their application to chemistry in the form of femtochemistry has made it possible to make observations on species that have such short lifetimes. This is how a typical experiment works:
Fig. 3: Femtosecond spectroscopic results for the reaction in which NaI separates into Na and I. The full circles (lower set of data) are the absorption of the complex and the open circles the absorption of the Free atoms (A.H. Zewail, Science, 242 (1988) p.1645). The bound Na absorption intensity shows up as a series of pulses that recur in about 1 ps, showing that the complex vibrates with about that period. The decline in intensity shows the rate at which the complex can dissociate as the two atoms swing away from each other. The complex does not dissociate on every outward-going swing because there is a chance that the I atom can be harpooned again, in which case it fails to make good its escape. The free Na absorption also grows in absorption oscillating manner, showing the periodicity of the vibration of the complex, each swing of which gives it a chance to dissociate. The precise period of the oscillation in Nal is 1.25ps corresponding to a vibrational wavenumber of 27 cm-1 (recall that activated complex theory assumes that such a vibration has a very low frequency). The complex survives for about ten oscillations. In contrast, although the oscillation frequency of NaBr is similar, it barely survives one oscillation.
[ TOP ]
(2-3) A thermodynamic approach to the Activated Complex Theory
The statistical thermodynamic version of activated complex theory rapidly runs into difficulties because only rarely is anything known about the structure of the activated complex. However, the concepts that it introduces, principally that of an equilibrium between the reactants and the activated complex, have motivated a more general, empirical approach in which the activation process is expressed in terms of thermodynamic functions. If we accept that: is an equilibrium constant (despite one mode of C‡ having been discarded), we can express it in terms of a Gibbs energy of activation, D‡G0 i.e.: i.e.: or:
But the Gibbs energy of activation can be divided into:
Under this classification, we can absorb the k term into the entropy term to obtain: But we have defined the activation energy for a reaction in the gaseous state as: where: i.e.: i.e.: i.e.: Thus: which is once again in the form of the Arrhenius equation, where the Arrhenius is given by: The entropy of activation is negative because two reactant species come together to form one species. However, if there is a reduction in entropy below what would be expected for the simple encounter of A and B, then the Arrhenius factor A will be smaller than that expected on the basis of simple collision theory. Indeed, we can identify that additional reduction in entropy, D‡S0steric , as the origin of the steric factor of collision theory, and write: Thus, the more complex the steric requirements of the encounter, the more negative the value of D‡S0steric, and the smaller the value of P. NOTE: Gibbs energies, enthalpies, and entropies of activation are widely used
to report experimental reaction rates, especially for organic reactions
in solution. They are encountered when relationships between equilibrium
constants and rates of reaction are explored using correlation analysis,
in which ln K (which is equal to D‡G0
/
RT
)
is plotted against ln k2 (which is proportional to DrG0
/
RT).
In many cases the correlation is linear, signifying that, as the reaction
becomes thermodynamically more favourable, its rate constant increases
(see fig. 4).
This linear correlation is
the origin of the alternative name linear free energy relation, LFER, that
is sometimes given
Fig. 4: For a related series of reactions, as the magnitude of the standard reaction Gibbs energy increases, so the activation barrier decreases. The approximate linear correlation between D‡G and DrG0 is the origin of linear free energy relations. Note how a high value of D‡G for reaction (a) correlates with a low value of |DrG0| (for that reaction (green), but a smaller value of D‡G, as for reaction (b) (red) correlates with a larger value of |DrG0|.
[ TOP ]
The thermodynamic approach to the activated complex theory simplifies the discussion of reactions in solution. The statistical thermodynamic theory is very complicated to apply because the solvent plays a role in the activated complex. In the thermodynamic approach we combine the rate law: with the thermodynamic equilibrium constant: i.e.: Let us now define ko2 as the rate constant with the activity coefficients equal to 1, i.e.: At low concentrations the activity coefficients can be expressed in terms of the ionic strength, I, of the solution by using the Debye-Huckel limiting law (see P.W. Atkins, Physical Chemistry, 6th Ed. Section 10.2c, particularly eqn 10.19) in the form: where A = 0.509 in aqueous solution at 298 K and zJ is the charge numbers on particle J. Thus,
Conversely, if reactant ions have opposite same signs, the charges in the activated complex cancel out and the complex has a less favourable interaction with its atmosphere than the separated ions with a solution of a high ionic strength. >> TECHNICAL NOTE: A plot of log(k/k0)
vs. l1/2 should be linear wheer the gradient gtives infomation
about the charge type of the activated complex for the rate determining
step. (see Fig 5 below).
Fig. 5: Experimental tests of the kinetic salt effect for reactions in water at 298 K. The ion types are shown as spheres, and the slopes of the lines are those given by the Debye-Hückel limiting law and the Kinetic salt effect equation above (Eqn. K.Salt.Effect). |
| E-mail me at jgri1@um.edu.mt |