Number of Different Solutions to the
Towers of
Jaroslav Sklenar,
Introduction
http://en.wikipedia.org/wiki/Tower_of_Hanoi
http://www.cut-the-knot.org/recurrence/hanoi.shtml
http://mathworld.wolfram.com/TowerofHanoi.html
and
many other. The problem can also be used to demonstrate the power of Dynamic
Programming. To learn more read the paper by Moshe Sniedovich at http://archive.ite.journal.informs.org/Vol3No1/Sniedovich/
where Dynamic Programming has been used to find the length of the shortest
solution and also the length of the almost ignored longest solution (and much
more). Here we use the Dynamic Programming approach to find the number of
different solutions to the problem.
I have arrived to this result myself, but I
think that I am not the first. Please let me know any reference to a source
where this formula has been published. It will be my pleasure to quote it.
Theory
Here
I assume that the reader is familiar with the problem, so just a brief summary:
The
three platforms (poles) are called L
(left), C (center) and R (right).
Tower is a collection of disks (rings) placed one on top of
other such that always a smaller disk is placed on a bigger one. Initially a
tower of height n made of disks 1…n of increasing size, where 1 is the top
smallest disk, is located in platform L.
Rules: when moving the disks we have to follow these rules:
-
only one disk at
a time can be moved
-
a disk may be placed
either on an empty platform or on a bigger disk.
Problem: we want to move the tower made of disks 1…n from the platform L to the platform R
by following the rules.
State of the game is given by three mutually exclusive sets
such that 
. A feasible state is such that can be reached by following
the rules. This also guarantees that these sets are either towers or they can
be empty. The initial state is 
, the final state is 
.
Solution is a sequence of moves (alternatively a sequence of
states generated by these moves) that solves the above problem by following the
rules. We consider only solutions without cycles where each state appears
mostly once.
Let
F(n,a,b,c) be the total number of different
solutions to the problem of moving a tower of height n from the platform a to
the platform b by using the platform c. As there is no difference between the
platforms with respect to the rules, we can use F(n) for short.
Theorem: F(n) can be computed by the recursive
formula
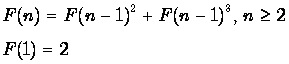
Proof:
For n = 1 there are clearly two
solutions without cycles: move the disk from L to R or move the disk from L to
C and then from C to R. Now we assume 
. To reach the final state the largest disk n has to be moved from L to R. This can
be done (always without cycles) in two different ways that we treat separately.
1) Move the tower (n-1)
from L to C, move the disk n from L
to R, move the tower (n-1) from C to
R. Moving the tower (n-1) from L to C
has F(n-1) different solutions, moving the tower (n-1) from C to R has also F(n-1) different solutions. These two
moves of the towers of height (n-1)
are independent, so the first case results in F(n-1)2
different solutions.
2) Move the tower (n-1)
from L to R, move the disk n from L
to C, move the tower (n-1) from R to
L, move the disk n from C to R, move
the tower (n-1) from L to R. We see
that there are three independent moves of the tower (n-1), so the total number of different solutions in this case is F(n-1)3.
As
the cases 1) and 2) are mutually exclusive, we have the total number of
different solutions given by the theorem formula. ˙
Legends
There
is a legend probably invented from scratch together with the game itself in
1883 by the French mathematician Edouard Lucas:
“Legend has it
that a group of Eastern monks are the keepers of three towers on which sit 64
golden rings. Originally all 64 rings were stacked on one tower with each ring
smaller than the one beneath. The monks are to move the rings from this first
tower to the third tower one at a time but never moving a larger ring on top of
a smaller one. Once the 64 rings have all been moved, the world will come to an
end”.
(For
more see the page http://hanoitower.mkolar.org from where the legend was taken).
It
is well known that an optimal solution to the game of n towers takes 2n-1
moves. Assuming that one move takes 1 second, after some simple calculation we
arrive to the result that the solution for n
= 64 takes about 585x109 years.
We
can offer another legend:
“Take only 5 rings and try all possible solutions.
Then the Universe will come to an end”.
If
we take an (unrealistic) assumption that each solution takes on average (they
have different lengths) only 1 second, it would take about 89.67x1020
years to try them all. Enough time for many big bangs.
Yet
another legend:
“Take only 4 rings and let each human on Earth solve
the game in different way. When all different solutions are used the Universe
will come to an end”.
In
past no end of Universe at all, but now this has changed. Still we have almost
one solution for each human.
Results
These
are numbers of solutions for increasing tower height:
F(1)
= 2
F(2)
= 12
F(3)
= 1872
F(4)
= 6,563,711,232
F(5)
≈ 2.827798101718050e+029
The
following are all the solutions for towers of height 1,2 and 3 (extract). Each
row contains one solution starting by its number. Moves separated by spaces
have the format:
kAB
where
k is the disk number that we move
from platform A to platform B. Note that the first solution is the shortest one
with 2n-1 moves, the last
solution is the longest one with 3n-1
moves.
1 (tower
height)
2 (number of
generated solutions)
1 1LR
2 1LC 1CR
2 (tower
height)
12 (number of
generated solutions)
1 1LC 2LR
1CR
2 1LC 2LR
1CL 1LR
3 1LR 1RC
2LR 1CR
4 1LR 1RC
2LR 1CL 1LR
5 1LR 2LC
1RL 2CR 1LR
6 1LR 2LC
1RL 2CR 1LC 1CR
7 1LR 2LC
1RC 1CL 2CR 1LR
8 1LR 2LC
1RC 1CL 2CR 1LC 1CR
9 1LC 1CR
2LC 1RL 2CR 1LR
10 1LC 1CR
2LC 1RL 2CR 1LC 1CR
11 1LC 1CR
2LC 1RC 1CL 2CR 1LR
12 1LC 1CR
2LC 1RC 1CL 2CR 1LC 1CR
3 (tower height)
1872 (number of
generated solutions)
1 1LR 2LC
1RC 3LR 1CL 2CR 1LR
2 1LR 2LC
1RC 3LR 1CL 2CR 1LC 1CR
3 1LR 2LC
1RC 3LR 1CR 1RL 2CR 1LR
4 1LR 2LC
1RC 3LR 1CR 1RL 2CR 1LC 1CR
5 1LR 2LC
1RC 3LR 1CR 2CL 1RC 2LR 1CR
6 1LR 2LC
1RC 3LR 1CR 2CL 1RC 2LR 1CL 1LR
7 1LR 2LC
1RC 3LR 1CR 2CL 1RL 1LC 2LR 1CR
8 1LR 2LC
1RC 3LR 1CR 2CL 1RL 1LC 2LR 1CL 1LR
9 1LR 2LC
1RC 3LR 1CL 1LR 2CL 1RC 2LR 1CR
10 1LR 2LC
1RC 3LR 1CL 1LR 2CL 1RC 2LR 1CL 1LR
11 1LR 2LC
1RC 3LR 1CL 1LR 2CL 1RL 1LC 2LR 1CR
12 1LR 2LC
1RC 3LR 1CL 1LR 2CL 1RL 1LC 2LR 1CL 1LR
13 1LR 2LC
1RL 1LC 3LR 1CL 2CR 1LR
14 1LR 2LC
1RL 1LC 3LR 1CL 2CR 1LC 1CR
15 1LR 2LC
1RL 1LC 3LR 1CR 1RL 2CR 1LR
16 1LR 2LC
1RL 1LC 3LR 1CR 1RL 2CR 1LC 1CR
17 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RC 2LR 1CR
18 1LR 2LC
1RL 1LC 3LR 1CR 2CL 1RC 2LR 1CL 1LR
19 1LR 2LC
1RL 1LC 3LR 1CR 2CL 1RL 1LC 2LR 1CR
20 1LR 2LC
1RL 1LC 3LR 1CR 2CL 1RL 1LC 2LR 1CL 1LR
. . .
1865 1LC 1CR
2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LR
2LC 1RL 2CR 1LR
1866 1LC 1CR
2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LR
2LC 1RL 2CR 1LC 1CR
1867 1LC 1CR
2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LR 2LC
1RC 1CL 2CR 1LR
1868 1LC 1CR
2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LR
2LC 1RC 1CL 2CR 1LC 1CR
1869 1LC 1CR
2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LC
1CR 2LC 1RL 2CR 1LR
1870 1LC 1CR 2LC
1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LC
1CR 2LC 1RL 2CR 1LC 1CR
1871 1LC 1CR
2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LC
1CR 2LC 1RC 1CL 2CR 1LR
1872 1LC 1CR
2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LC
1CR 2LC 1RC 1CL 2CR 1LC 1CR
You
can download a text file with all solutions for the
tower of height 3.
The number of different solutions for even small towers is impressive. To check the formula I have written programs in Turbo
Pascal 7 that generate the solutions in a text file in the above format, check
whether the solutions are all different and simulate them to check whether they
are correct. They can be used also for manually created solutions. If you want
you may download these programs. All should be clear
from comments in the source files.
This
article is translated to Russian
language by Kerstin Schmidt.
This article is translated to Finnish language by Elsa Jansson.
This article is translated to Estonian language by Martin Aus.