Random variables with user defined (empirical table) distribution are generated by the so-called Inversion that is also called "inverse function method". The user has to enter the table of the cumulative distribution function (CDF) F(x) also known as the "Distribution function". To generate a new random value the program first generates a normalized random variable U uniformly distributed on the interval (0, 1). The random value y is then computed as y = F -1(U). This is implemented by searching the F(x) table for the first entry whose F(x) value is greater or equal to U. The program then returns either the corresponding value x (discrete random variables) or performs linear interpolation using the previous table entry (continuous random variables).
Example: Assume the following random distribution:
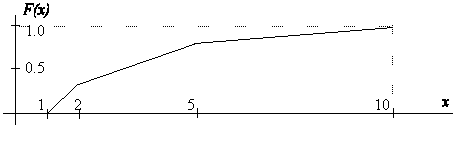
| x | 1 | 2 | 5 | 10 |
|---|---|---|---|---|
| p(x) | 0.0 | 0.3 | 0.5 | 0.2 |
| F(x) | 0.0 | 0.3 | 0.8 | 1.0 |
Graphically:

The value 0.55 of the normalized random variable U will produce either the random value 5 (discrete random variable) or 3.5 (continuous random variable).
For the generator to work properly these rules have to be satisfied:
The method is very general., practically any distribution can be entered. If two adjacent table entries have the same x value, that value will be generated with the probability given by the difference of the F(x) values, both for discrete and continuous mode of generation. In this way it is possible to generate a general random variable with a continuous distribution, but with some values having nonzero probability. If two adjacent table entries have the same F(x) values, the values from the interval given by the two x values will be never generated. In this way it is possible to generate for example bimodal random variables.
The table can be entered in two ways. Either as a sequence of the values with their probabilities or directly as the points of the cumulative distribution function. In both cases there is validation with self-explaining messages. Validation is partially suppressed during editing table entries to allow temporarily inconsistent tables. To start simulation that uses a user defined distribution, the table has to be confirmed. Confirmation also validates the table for consistency. During validation the values of the distribution function F(x) can be truncated to 1, the last value can be set to 1. In the table only 10 decimal places are displayed, but the values in memory are not truncated.
Note that editing operations work differently when entering probabilities or cumulative distribution respectively. When entering probabilities, the cumulative distribution values are always calculated as sums of probabilities - it may happen, that the value gets above 1 (it can be adjusted later). When entering cumulative distribution the values of probabilities are calculated as differences of adjacent cumulative probabilities. The table may be temporarily inconsistent with negative values of probabilities. Confirmation always checks the table consistency.
The mode can be changed at any time, for example the table can be initially entered using probabilities and then modified by changing values of the cumulative distribution.
The generator can work in two modes that produce values of either a discrete or a continuous random variable. In the discrete mode the random generator returns only values entered in the distribution table. In the continuous mode the generator performs linear interpolation that approximates "continuous" distributions. Arrival intervals and service duration are typically continuous random variables, but some servers may work in such a way that there are few more or less constant service times (a car wash line with various programmes).
The Save button saves the table to a cookie. Table status is also saved, so it is possible to save not finished (inconsistent) tables. The cookie contains values and cumulative distribution. Probabilities are computed after loading (Load button) as differences between adjacent values of cumulative distribution. If possible, save confirmed consistent tables. Generation mode (continuous/discrete) is also saved. The cookie expiration is one year, then the cookie will be deleted by the browser. Check (Save and immediately Load) whether your browser enables cookies.