Exercise 2

Contents

• Exercise 2.1
• Exercise 2.2

big(bear).
big(elephant).
small(cat).
 
brown(bear).
black(cat).
grey(elephant).

(b) Trace the execution of the goals:

?- big(X), dark(X).
 
?- dark(X), big(X).

?- trace.
      

(c) Write a relation to test and display how many times the predicates big, small, brown, black and grey are used in the above.

1. First add the following line at the top of your prolog file:

   :- ['/home/mros/www/prologcc/code/utils'].
         

   This causes the following definitions to be loaded.
   • initcounter(V) - initialise counter
   • inc(V) - increment counter
   • writev(V) - write the value of counter.
   Example

   ?- initcounter(foo), inc(foo), writev(foo).
   foo = 1
   Yes
   

2. Modify the definition of each fact so as to increment the relevant counter.
3. Define a test predicate which sets up the counters, calls the relevant goals, and prints the results.

1. Create a working directory for this problem and copy all the .pl files in /home/mros/www/prologcc/code to that directory
2. Use prolog facts to create a representation of the underground map above. One way of doing this is to create, for each station, a fact relating that station to a list of all the stations that are immediately accessible, e.g.

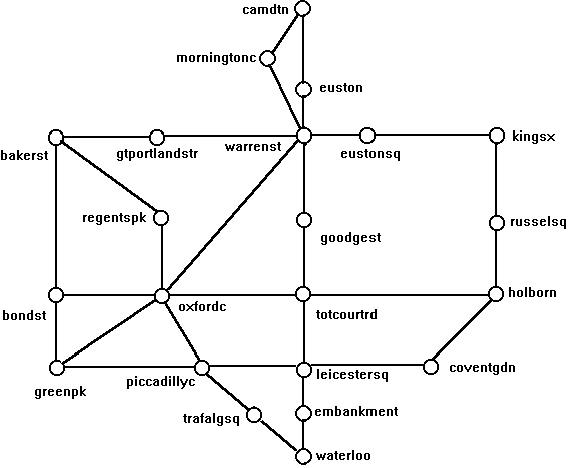
   link(bondst,[bakerst,greenpk,oxfordc]).
   	  

   N.B. The data is present in the files you copied (tube.pl) if you want to make use of it.
3. Run prolog and load ex0202.pl, which defines the following:
   • bfs(Start,Goal,Solution) (breadth-first search)
   • dfs(Start,Goal,Solution) (depth-first search)
   • dls(Start,Goal,Limit,Solution) (depth limited search).
   Try to figure out the maximum length path that can be handled using bfs and dfs. Be patient and if no solution is forthcoming, note the kind of error message (there are two different ones of interest). Finally, try using dls for progressive increasing depth.

   Here is an example of what happens when the search terminates successfully.

   6 ?- bfs(wrs,tcr,S). 
   S = n(tcr, n(gdg, n(wrs, 0, 0), 1), 2) 
    
   	      

   The query means: find a path from wrs (warren st) to tcr (tottenham ct. rd) and bind the solution node to S. In this case the search succeeds. Note carefully the format of the solution, which is a search node.
4. Define ids in terms of dls. In order to do this you will need to use a recursive definition. The general ideas behind such definitions are to be found in tutorial 3.
5. Define a predicate which, when given a node, prints out the corresponding search path, eg.

   ?- bfs(wrs,tcr,S), show_path(S).
   wrs - gdg - tcr
   

   You will also need to find out about the built in predicates write, nl, and for the more ambitious, format. Help on all such built-ins can be accessed from Prolog using

   ?- help(predicate-name).
   	  

6. The second part of the file ex0202.pl defines a predicate which, given a solution node, shows the path and then prints some statistics about the solution, namely, the number of nodes generated, the number of nodes expanded, and the maximum no. of nodes helpd in memory at any one time. If you try to invoke this predicate it always returns 0 for these numbers:

   3 ?- bfs(cmt,wrs,S), show_solution(S).
    
   solution path is: cmt - eus - wrs
   no. of nodes generated = 0
   no. of nodes expanded = 0
   max. no. of nodes in memory = 0
   S = n(wrs, n(eus, n(cmt, 0, 0), 1), 2) 
   

   In order to make it work properly, calls to set the the relevant counters (nodes_generated and nodes_expanded, nodes_in_mem, max_nodes_in_mem) must be inserted at appropriate points in the file search.pl.

   The exercise is to examine the file search.pl and discover where to set the counters

   Hint: You will need to use the following predefined predicates to set the variables. All of them are defined in utils.pl.

   • inc(V) - increment variable V
   • dec(V) - decrement variable V
   • setmax(V,MAX) - if current value of V is greater than MAX, set MAX to V (otherwise do nothing).

where S is the name of the state, P is the parent and D is the depth, so the solution node here has state tcr (which is the goal), depth 2 and parent n(gdg, n(wrs, 0, 0), 1)), i.e. a node with state gdg, depth 1 and parent , which is the initial node. By convention, this has parent 0 and depth 0 (see the predicate make_initial_node in search.pl).