1. The internal energy

• Open, closed and isolated systems
• Heat and work - the sign conventions
• Internal energy and internal energy changes, U and DU
• State functions
• The first law of thermodynamics

Open, closed and isolated systems:
 

OPEN SYSTEM	CLOSED SYSTEM	ISLATED SYSTEM

 
 

	Open Systems	Closed Systems	Isolated Systems
Exchange of contents with surroundings	Yes	No	No
Exchange of heat with surroundings	Yes	Yes	No

 
 

Heat and work - the sign conventions:

• Heat
• Work
• Work done on a system, or by a system 
• P-V work
• Expansion of a gas at contant temperature
• Reversible expansion of an ideal gas

• A form of energy that can be transferred as a result of a temperature difference (see fig. 1)
• Should be considered as a DISORDERED form of energy
• Can be measured in terms of the heat capacity. For example:

where c_s is the specific heat capacity (i.e. the heat capacity per unit mass) and  c_M is the molar heat capacity (i.e. the heat capacity per mole).  TO BE REVISITED.



Fig. 1: Heat energy transfer 

• Work is done as a result of motion or mechanical change, i.e. a direct result of the action of a force.
• Should be considered as an ORDERED form of energy
• Mathematically given by: 
w = force x distance moved

• Note: 
• NEGATIVE work is work done BY a system
• POSITIVE work is work done ON a system

Since P_ext = Force / cross-sectional area, then:

Note: 

1. The Negative sign is due to the fact that dx is in the opposite direction of P_ext . 
2. The Negative sign in the overall work indicates that work is being done by the system.

---

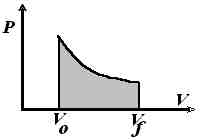
[ TOP ]

(a) Expansion of a gas at a constant pressure

1. Push piston inwords to compress the gas
2. Release it => expanion agains a constant pressure,  P_ext 

---

[ TOP ]

(b) Reversible expansion of an ideal gas

NOTE: REVERSIBLE PROCESS => MAXIMUM WORK

1. Push in piston rapidly by increasing P_ext 
2. Allow gas to expand slowly by reducing the push on the piston (i.e. P_ext )

If expansion takes place very slowly, P_ext is slighly lower than P_int at all times, i.e. P_int =P_ext + DP. In the limit when DP goes to zero, the process becomes reversible. 

Internal energy and internal energy changes, U and DU
 

The internal energy of a system, U, is the total energy of the system, i.e. the sum of the potential energy (PE) and kinetic energy (KE).

(i) The PE is due to the chemical bonds and inter/intermolecular forces. This contribution is even present at 0K
(ii) The KE is due to motion - vibrations in solids rotations and translations in fluids. The KE is 0 at 0K.
 

Note: 

(1) Estimates of the internal energy may be obtained from statistical thermodynamics (e.g. in molecualr modelling).

(2) Rather than the absolute values of the internal energy (U), we usually speak of changes in the internal energy, DU.

(3) See also the first law of thermodynamics.
 

State Functions:

A state function refers to a property whose 'value' depends solely on the state of the system, and NOT dependent on the way that this state is achieved. In particular, the work done, w, and heat energy transferred, q, are NOT state functions (see fig. 1), whilst the internal energy U is. 

The most commonly used feature of a state function, (U, for example), is that we may write:
 

............................................................... (eqn. 1)

that is the change in 'U' between state '1' and state '2' is the difference between value of 'U' in state '2' (=U₂) and the value of 'U' in state '1' (=U₁).

Another important property of state functions, is that a function which is solely composed from other state functions is itself a state function. composed up from sum of two or more state functions. For example, since U, P and V are state functions, the enthalpy H defined as below is also a state function.
 

...............................................................(eqn. 2)

We shall now present the properties of state function in the rigour of the mathematical notation:
 
 

(1) Integration of a state function U must have a definite value which is independent of the path of integration (in between the limits A and B). 
 

...............................................................(eqn. 3)

This means that dU is an exact differential. 
 
 

(2) Since U is an exact differential, if U is determined by the values of the variables x and y, then:
 

................................ (eqn. 4)

where 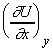 is the rate of change of U with respect to x, keeping y constant.
 

(3) The order of differentiation of a state function is immaterial, i.e.: 
 

.................................. (eqn. 5)

The first law of thermodynamics

The first law of thermodynamics states:
          DU = DQ + Dw
i.e. the total energy of a system is constant.

          DU = DQ - p_exDV

          DU = DQ + 0  = DQ |_V

>> Note the terms (x)_y or x|_y mean 'the value of 'x' at constant 'y'.

(3) In gases, at ISOTHERMAL conditions, we have:

DU = 0 = DQ + Dw   =>  DQ = -Dw

This is beacuse:

(1) at isothermal conditions, the KE contribution remains constant
(2) in gases, the PE contribution is constant due to the very large intermolecular distances, and hence lack of interactions. 

It means that:

(1) Isothermal expansion has to be accompanied by a heat absorption
(2) Isothrmal compression has to be accompanied by heat losses.