The heat capacities:
We saw in section 1 that we may quantify the amount of heat transfer Dq through the following relation:
where: n is the number of moles, c is the molar heat capacity, and DT is the resulting change in temperature.
However, although this elementary treatment is usually sufficient for the treatment of solids and liquids, the heat capacity for gases is highly dependent on the conditions of the experiment. In view of this we shall introduce two more specific heat capacities
(i) The molar heat capacity constant pressure, cp
(ii) The molar heat capacity constant volume, cv
Further more, although for most cases we assume that these heat capacities are constant values over the temperature range of interest, we shall also show how a more accurate estimation of the heat capacities may be achieved by expressing them as functions of temperature.
In our discussion below, we shall assume that n=1 for simplicity.
The heat energy transfer at (i) constant pressure and (ii) constant volume may be related to the resulting change in temperature as follows:
(i)
(ii)
We may thus write:
(i) 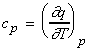
and (ii)
whilst from our discussion of enthalpy H and internal energy we have:
(i) 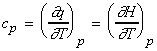
(ii)
Let us now consider the temperature variance of the heat capacities:
(1) Elementary treatment of the heat capacities - the heat capacities are constant in the range of interest.
If the assume that cp and cv is constant at the range of temperature (T1,T2), then we may write cp and cv as mean cp and cv , i.e.:
(2) More advanced treatment of the heat capacities - the heat capacities are functions of temperature.and
We may write cp and cv as functions of temperature by fitting a polynomial of order m, i.e.:
or:
Note: (a) For most cases we assume m=2 (i.e. quadratic) gives
a reasonable description of heat capacities, (b) In the elementary treatment,
we assume that the coefficients b,
c,… are zero.
IMPORTANT NOTES:
(1) The molar heat capacities a constant pressure and constant volume are related by the following relationships:
(i)where g is the heat capacity ratio, which is encountered in the equation for an adiabatic (i.e. no exchange of heat) reversible expansion of a perfect gas, i.e.: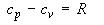
(ii)
(2) For a monatomic perfect gas, cv = 3R/2,
whilst for a polyatomic non-linear molecule, cv = 3R.