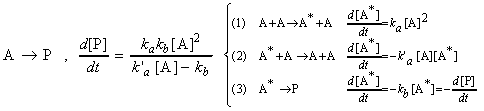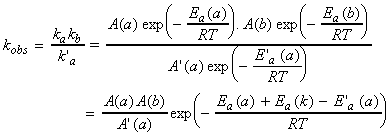Chemical kinetics for various processes (iii)
The Relationship between the overall
rate constant of a composite reaction (Examplified through the
Lindemann-Hinshelwood mechanism)
See also: Derivation of the rate law for The Lindemann-Hinshelwood Mechanism - First-order gas phase kinetics - Unimolecular Reactions
The Relationship between the overall rate constant of a composite reaction (Examplified through the Lindemann-Hinshelwood mechanism)
The Lindemann-Hinshelwood mechanism (as many others) contains a number of individual elementary steps, for each of which its own activation energy, and hence a different type of relationship with temperature. This poses an important question: we know that all individual rates are likely to increase with an increase in temperature, but is this true for the overall rate? We shall attempt tackle this important question by considering the specific case of the Lindemann-Hinshelwood mechanism, which as we have seen has a rate law given by:
where the rate constants corresponds to the following steps in the reaction A -> P:
which if v(2)>>v(3), we get:
Now, each of these three rate constants for the elementary steps
can be written in terms of its associated activation energy through an
Arrhenius equation. Thus the overall rate constant is given by:
This means that the overall rate constant kobs
has an Arrhenius-like form with an activation energy:
This means that, with an increase in temperature, the overall rate
will:
> (a) Increase if Ea(obs) is positive, (see fig. 1a) i.e.:
Although this (i.e. that the rate of a reaction decreases with an increase in temperature) may sound strange, all it means is that reaction (2) (i.e. the reverse reaction) is so sensitive to temperature, that its rate increases sharply with an increase in temperature. (Note that this latter condition is very unlikely in the particular case of the Lindemann- Hinshelwood mechanism, although this condition is encountered in some other reactions which a similar mechanism.)> (b) Decrease if Ea(obs) is negative, (see fig. 1b) i.e.:
Notes:
(1) The fact that for most reactions we observe an Arrhenius-like behaviour demonstrates that most reactions have a very simple rate law, e.g. v = ka[A]2 .
(2) However for some equations, the relationship between rate and temperature
is very complicated. For example, in an enzyme reactions, the enzymes may
become denatured as the temperature increases, hence halting the reaction.
Fig. 1: For a reaction with a pre-equilibrium, there are three activation energies to take into account, two referring to the reversible steps of the pre-equilibrium and one for the final step. The relative magnitudes of the activation energies determine whether the overall activation energy is (a) positive or (b) negative.