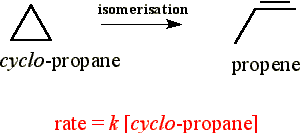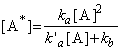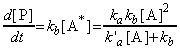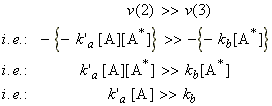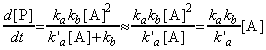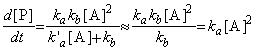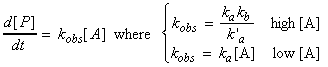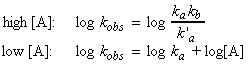Chemical kinetics for various processes (ii)
The Lindemann-Hinshelwood Mechanism - First-order gas phase kinetics - Unimolecular Reactions
Important Aside: The
Relationship between the overall rate constant of a composite reaction
(Examplified through the Lindemann-Hinshelwood mechanism)
The Lindemann-Hinshelwood Mechanism - First-order gas phase kinetics - Unimolecular Reactions
NOTE: 'Unimolecular reactions' usually refer to first-order gas phase reactions. This is because these reactions involve a unimolecular step in which the reactant molecule changes to product. However, it should be noted that the overall mechanism involves bimolecular as well as unimolecular steps.
A number of gas phase reactions such as:
follow first order kinetics. This observation poses one obvious question - reactions usually occur through collisions, and by default, collisions are bimolecular events, so how can there be a first-order rate law?
The first successful explanation of unimolecular reactions was provided
by Lindemann way back in 1921. This mechanism was later elaborated by Cyril
Hinshelwood, and is hence now known as the Lindemann-Hinshelwood mechanisms,
and is illustrtaed in Fig. 1.
Fig. 1: A representation of the Lindemann-Hinshelwood mechanism of unimolecular reactions. The species A is excited by collision with A, and the excited A molecule (A*) may either be deactivated by a collision with A or go on to decay by a unimolecular process to form products.
According to the Lindemann-Hinshelwood mechanism (see fig. 1), the reaction takes off by having a molecule A getting energetically through a collision with another A molecule:
The energized molecule A* might loose is excess energy either by:
(1) Collision with another A molecule (forming no products), i.e.:
(2) Shaking itself apart forming the product (the unimolecular step), i.e.:
If this last unimolecular step is slow enough such that it becomes
the rate-determining step, then the overall reaction will have first-order
kinetics. This can be demonstrated by applying the steady state approximation
to the formation of A*:
which assuming equality solves to:
i.e. the rate of formation of P (which for now is not first-order) is given by:
Now if we assume that the rate of the reaction (2) is much greater than that of (3), i.e.:
(Note that this is particularly true at high concentrations (partial pressures) of A).
Then the rate of formation of the products will assume a first-order form, i.e.:
i.e.:
That this last equation is only valid when k`a[A] >> kb. Thus, if the concentration of [A] (i.e. the partial pressure) is reduced, then this assumption does not remain valid and instead at very low concentrations of A, we start getting k`a[A] << kb , i.e:
This means that if we let:
This means that is we take logs of both sides for the equation of kobs we get:
If we plot log kobs vs. log[A], we should get two straight line curves one at high concentrations with gradient 0 showing that kobs is a constant, and one for low A concentrations, with gradient 1 (see fig. 2).
Note: We get two important advantages by taking logs of both sides: (1) the data for the lower concentrations gets more spaced out, and more importantly, (2) we get a big change in the gradient - from 0 at high [A] concentrations, to 1 at low concentrations.
Fig. 2: A plot of the concentration dependence of the unimolecular
rate constant for the isomerization reaction of methyisocyanide at 427.5K.
(Ref: D. A McQuuarrie and J.D. Simon, Physical Chemistry, A molecular
Approach, University Scince Books, Saualito, CA, ISBN 0-935702-99-7)
Important Aside: The Relationship between the overall rate constant of a composite reaction (Examplified through the Lindemann-Hinshelwood mechanism)