collision_theory

CH237 - Chemical Thermodynamics and Kinetics

Dr. Joseph N. Grima, Department of Chemistry
University of Malta, Msida, MSD 06, MALTA
http://staff.um.edu.mt/jgri1/teaching/ch237

BACK TO TABLE OF CONTENTS

A theoretical investigation of chemical kinetics - Derivation of the rate constant from first principles (ii)

(1) Reactive encounters:

(0) Aside- The kinetic Theory (on a separate page)
(1-1) Reactive encounters in the Gas Phase (The Collision Theory)
         (1-1-0) Introduction
         (1-1-1) The encounter rate.
         (1-1-2) The minimum energy requirment
         (1-1-3) The steric factor.
         (1-1-4) Obtaining the rate constant.

(1-2) Reactive encounters in the Liquid Phase
         (1-2-0) Introduction
         (1-2-1) Diffusion-controled reactions
         (1-2-2) Activation-controled reactions

[ TOP ]

(1-1) Reactive encounters in the Gas Phase (The Collision Theory)

In this section we shall attempt to derive from first principles an expression for k₂, the rate constant for the gas-phase bimolecular elementary reaction below:

We can anticipate that the factors that we should consider are:

The encounter rate, that is the rate of collisions - the higher the frequency of collisions between A and B, the higher is the chance of a reaction taking place.
The minimum energy requirement - a collision will only lead to a reaction, it the energy of A and B (the KE) exceeds a minimum value, the activation energy.
The steric requirement - In some cases, reaction will only occur if the reactants collide in some particular orientation.

Hence we may deduce that:

[ TOP ]

(1-1-1) The encounter rate.

In this section we shall derive an expression for the collision density, Z_AB which is defined as:

This is of course related to the collision frequency. We have already seen that the collision frequency, z, for a single A molecule of mass m_A in a gas of other A molecules is given by:

where s is the collision cross-section, and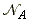

is the number density of A, given by:

N_A being Avogadro's number.

Given the collision frequency, z, we may calculate the collision density, Z_AA, that is the density of collisions between two A molecules in this gas. This is given by:

where the factor 1/2 is introduced to ensure that a collision is not counted twice. (When a A1 collides with A2, then inevitably, A2 collides with A1. However, this is only once collision.)

In analogy to all this, the collision density for an A with B collision is given by:

(The 1/2 factor has now been discarded because we are considering an A molecule colliding with any B molecule.)

In this case, the collision cross-section s is given by (see fig 1.):

and m is the reduced mass.

Fig. 1: The collision cross-section for two molecules can be regarded to be the area within which the centre of the projectile molecule (A) must enter around the target molecule (B) in order for a collision to occur. If the diameters of the two molecules are d_A and d_B, the radius of the target area is d = 1/2 (d_A + d_B) and the cross-section is pd².

[ TOP ]

(1-1-2) The minimum energy requirement

We can include the minimum energy requirement condition by expressing the collision cross-section as a function of e, the KE of approach (relative KE) of the two colliding species before collisions.

We shall set this cross-section s(e) as:

This function indicates that if we do not have the energy e_a (the threshold value of energy) then s(e)=0. Otherwise, the cross-section will have a value that depends on s and on e_a/e.

Thus for a collisions with a specific relative speed of approach v_rel we have:

where the relative KE, e, is related to the relative speed through:

i.e.:

However since a wide range of approach energies are present in the sample, we should average this expression, as in the case of the Maxwell-Boltzman distribution, i.e.:

(Note that in contrast with Z_AB , in this expression there is only one Avogadro's constant since we are now dealing with moles, i.e. we have to divide by N_A.)

Thus the problem reduces to evaluation of the integral:

Let us start by finding an expression for f(e)de. From the Maxwell-Boltzmann distribution for molecular speeds:

and from k = R / N_A and e = ½mv² i.e. de = mvdv, i.e.:

we note that:

i.e.:

where E_a is the activation energy.

[ TOP ]

(1-1-3) The steric factor

At this point we introduce a steric factor, P, and define the reactive cross-section s* as a multiple of the normal cross-section, (see fig. 2) i.e.:

(P is usually (though not always) several orders of magnitude smaller than 1, and in some cases, may be obtained from experiment.)

Fig. 2: The collision cross-section is the target area that results in simple deflection of the projectile molecule; the reaction cross-section is the corresponding area for chemical change to occur on collision.

[ TOP ]

(1-1-4) Obtaining the rate constant

Given all these expressions, we may re-write the rate equation as:

But we know that:

Thus we note that:

Note that this equation is in the form of the Arrhenius equation

provided that the exponential temperature dependence dominates the square root temperature dependence of the pre-exponential factor. It follows that the activation energy, E_a can be associated with the minimum KE along the line of approach that is needed for a reaction, and that the pre-exponential factor is a measure at which collisions occur in a gas.

[ TOP ]

(1-2) Reactive encounters in the Liquid Phase

Encounters between reactants in solution occur in a very different manner from encounters in gases:

Against: Because reactant molecules have to jostle their way through the solvent, so their encounter frequency is considerably less than in a gas.
For - The cage effect: Once the reactants have encountered each other stay, they near each other for a much longer than in a gas. This lingering of one molecule near another on account of the hindering presence of solvent molecules is called the cage effect. Such an encounter pair may accumulate enough energy to react even though it does not have enough energy to do so when it is first formed.

NOTE: The activation energy of a reaction in solution is a much more complicated quantity than in a gas because the encounter pair is surrounded by solvent and hence the energy of the entire local assembly of 'reactant + solvent' molecules must be considered.

Consider the reactions:

where AB signifies the 'encounter pair'. This reaction involves three 'steps':

(i) the formation of the encounter pair AB form A and B;
(ii) The encounter pair may break again to A and B up without reaction,
(iii) The encounter pair may form the product P.

Thus we have:

Using the steady state approximation we have:

i.e. assuming equality:

i.e.:

i.e. The rate of formation of P is given by:

i.e.:

Let us now consider two scenarios:

(1-2-1) A diffusion-controlled reaction, when k_a >> k'_d
(1-2-2) An activation-controlled reaction, when k_a << k'_d

[ TOP ]

(1-2-1) A diffusion-controlled reaction, when k_a >> k'_d, that is once AB has been formed, then the rate of re-separation of the unreacted encounter pair is much slower than that for the formation of the products. In such case we have:

In this diffusion-controlled limit, the rate of reaction is governed by the rate at which the reactant molecules diffuse through the solvent.

An indication that a reaction is diffusion-controlled is that its rate constant is of the order of 10⁹ Lmol^-1s^-1 or greater. Radical and atom recombination reactions are often diffusion-controlled since the combination of radicals involves very little activation energy.

This rate of reaction is calculated by considering the rate at which the reactants diffuse together. In particular, if we assume that a reaction will only occur if the two reactant molecules come within a distance R* from each other, then we have:

i.e.:

where D_A and D_B are the diffusion coefficients of the two reactants in solution, which can be estimated by the Stokes-Einstein equation as:

and

where h is the viscosity, i.e. (since k = R/N_A):

If we further assume that

, then we have:

In this approximation, the rate constant is independent of the actual reactants and depends only on the temperature and the solvent viscosity. It shows that the rate constant increases with increase in temperature and decreases with an increase in solvent viscosity (reactants find it more difficult to move through solvent).

[ TOP ]

(1-2-2) An activation-controlled reaction, when k_a << k'_d, i.e. when a substantial activation energy is involved in the reaction of AB to form P. In this case:

where K is the equilibrium constant for A + B = AB. In this case, the reaction proceeds at the rate at which energy accumulates in the encounter pair from the surrounding solvent.

BACK TO TABLE OF CONTENTS

[ UNIVERSITY OF MALTA | FACULTY OF SCIENCE | DEPARTMENT OF CHEMISTRY ]

E-mail me at jgri1@um.edu.mt

http://staff.um.edu.mt/jgri1