JSSim
JavaScript Discrete Simulation Tool
Version 2
Contents
2
Object-Oriented Programming in JavaScript
9
Input/Output General Guidelines
J. Sklenar
Department of Statistics and Operations
Research
Faculty of Science
University of Malta
JavaScript is a script language interpreted by web browsers. JavaScript is the original name owned by Netscape, a similar language is called JScript by Microsoft. Both are supposed to be compatible with the standard ECMA-262 that is also approved by the ISO as ISO-16262. That’s why the language is also called ECMAScript. Next the name JavaScript will be used. Compatibility with the ECMA standard does not guarantee equal behavior in all browsers, so it is suggested to check pages that use JSSim code in your favorite browser. Note also that currently JSSim supports only client-side applications.
JavaScript is
not a classical class-based strongly typed object-oriented language (OOL) like
for example Simula or Java. In fact it is the opposite. Nevertheless the object
model of JavaScript enables use of all important techniques of object-oriented
programming (OOP), either directly or with some additional support. For example
inheritance has to be programmed explicitly. That’s why the chapter 2 of this
manual shows how to use the techniques of object-oriented programming in JavaScript. Regarding other features of
the language, JavaScript contains everything that we expect in a high-level
language. Description of the language as such is of course out of the scope of
this manual.
A JavaScript programmer is thus making use of a modern programming language that, together with HTML, supports creation of documents that can contain user-friendly input of validated data, any kind of data processing, and lucid presentation of results. Solutions based on JavaScript and HTML are typically placed on the web and made thus available literally to everybody who has a browser supporting particular versions of these two languages. These capabilities have been applied to create various web-hosted problem-solving tools. Such tools can contain simple and medium-scale simulation models. Several simulation models have already been implemented and placed on the web with very encouraging response. Routines used to create these models, including a simple event-oriented simulation engine together with a collection of classes for general use in discrete simulation, have been collected into a tool called JSSim (JavaScript Simulation). This document is a JSSim manual that assumes that the reader is familiar with JavaScript and HTML.
2 Object-Oriented Programming
in JavaScript
In this chapter we assume that the reader is familiar with basic ideas of
object-oriented programming. A very fundamental introduction is available in my
Turbo Pascal page at: http://staff.um.edu.mt/jskl1/turbo.html#OOP
.
Everything is an object
Some authors would not call JavaScript an OOL, but in fact JavaScript programmer works only with objects and their methods and properties. If not stated explicitly, properties mean value attributes, but in JavaScript there is actually very little difference between value attributes – properties and procedure attributes - methods. Due to loose typing a property can become a method and vice versa. Most JavaScript “programs” are short snippets incorporated into HTML documents by using the tag <SCRIPT> that can also reference a separate file with JavaScript code (default extension js). JavaScript code is processed by the browser’s interpreter as a part of the (re)loading process. Such code typically defines functions and declares and initializes global variables. Using OOP terminology, such code is interpreted in the context of the so-called global object. For each browser window or each frame within a window a separate global object is created. So for example a global variable declared by the following statement:
var
expduration = 1000; //default experiment
duration
in fact creates (declares) a property of the global object that can be called directly by its name, but also as this.expduration or window.expduration. The keyword this is a reference (handle) of the current object. Similarly each global function declared by the user is a method of the particular global object. All standard properties and functions are also pre-defined properties of the global objects (for example mathematical functions and constants are accessible through the Math object that is an automatically created property of the global object). What about the statements written directly in <SCRIPT> tags? Here the best analogy is the “life” as defined for Simula class instances. There can be a lot of such code in several <SCRIPT> tags and in js files. All this code is performed in lexical order as the life of the global object (obviously without any possibility to break and postpone its execution). Interpreted JavaScript has only run-time; compile-time does not exist. Still there are two stages: (re)loading is a sort of early or first run-time stage. During this stage the programmer creates all global data that includes “declaration” of prototypes – see later, and creation of global object instances. Second run-time stage is made of execution of functions activated by browser events (like for example pressing a button). Even now, all is done in the context of the so-called call object. Each activation of a function creates a separate call object, so declaration of a local variable (say var x = 0;) in fact creates a property of the call object. Actual parameters of the function call are also considered as properties of the call object (there is another array property arguments that contains all parameters passed to the function, so in JavaScript it is possible to write functions accepting variable number of parameters).
Every function can be a constructor
In JavaScript object instances are created by the operator new similarly as in practically all OOLs:
queue = new
FifoQueue("q1”,0); // new queue
object
The difference between JavaScript and compiled OOLs is the fact that there is no class declaration in JavaScript. So the constructor has much more important role. Unlike constructors of compiled OOLs that basically just initialize the instance, JavaScript constructor actually creates (constructs) an instance by creating its properties and possibly methods. There is no special keyword to write constructors, so each function can potentially be a constructor. We already know that for each function call JavaScript creates a call object. It in fact creates another initially empty object (here we shall call it created object) that can be in the function body referenced by the keyword this. Functions that are not intended to be constructors ignore it. Note that call object and created object are really two distinct objects. For example consider the following statements anywhere in a function body:
var x =
1;
this.x
= 2;
alert(x);
The value displayed will be 1 (property of the call object), alert(this.x) would display 2 (property of the created object). A constructor function is not supposed to return any value, but it can. If it returns an object, the standard created object is ignored and the returned object will be used instead. But there is more: in JavaScript each function is in fact represented by a function object created during parsing a function. With respect to possible use of the function as a constructor, let’s call this object constructor object or simply constructor. Unlike the other two objects associated with a function call (call and created objects) that exist only temporarily during the function execution, constructor object is permanent (it is removed by loading another document). Because it is an object, it can have properties and methods. The most important one is prototype – see the next chapter. Using OOP terminology each constructor (and so each function) has - or can have - the same role as class declaration in compiled OOLs. Whether a particular function really represents a class depends only on its body (constructors are supposed to create properties by statements like the above one: this.x = 2;) and especially on its use after the new operator. Note that constructors can create value properties and methods in unified way:
Note that all instances created by the above constructor will have their own code of the method shift. The obvious requirement is a code stored only once for all instances. In JavaScript this is achieved by prototypes.
Prototypes
Prototype is the property of each function (constructor), so there is one prototype for every class (provided the function is used as a constructor). JavaScript enables objects (instances) to access prototype properties and methods in the same way as its own private properties and methods: o.m() activates the method m of the object o. It can be either private local method of the instance or a prototype method common to all instances of the class of o. Sharing prototype methods by all instances is no problem, but what about value properties? JavaScript avoids clashes and side-effects by making prototype value properties read-only. They are created and initialized at parse time; instances can only read their values. They can be useful as constants common to all instances of the particular class. Creating prototype properties (not typical) and prototype methods thus completes the class definition. Let's summarize: each class is represented by two permanent objects: constructor and prototype (constructor's property) and then there can be any number of instances that can have their own properties and methods and that can access properties and methods of the two permanent objects. Using the prototype paradigm the class point can be implemented in this way:
Now
the code of the method shift is stored only once with obvious consequence -
after its modification all instances will use the modified version.
Standard OOP techniques
The two previous paragraphs give a hint how to create the usual four types of properties and methods associated with a certain class:
Instance value properties are created by the constructor (or by a function called by the constructor – see later) using the handle this.
Instance methods can be created either directly by the constructor or preferably by the prototype – see the two above examples.
Class value properties that are associated with the class as such, not with the individual instances can be created as properties of the constructor:
point.count
= 0; // number of created points
Class constants can be properties of either the constructor:
point.maxX
= 800; // maximum x co-ordinate
or the prototype which ensures the read-only access:
point.prototype.maxX
= 800; // maximum x co-ordinate
Class methods associated with the class as such, not with the individual instances can be created as methods of the constructor:
point.distance = function(p1,p2)
{
var dx = p1.x - p2.x;
var dy = p1.y – p2.y;
return Math.sqrt(dx*dx + dy*dy)
};
Note that the above declaration is logical – distance applies to two points, so it is more natural to declare it as a class method and not as an instance method.
Inheritance
Let’s consider only instance value properties and instance methods and let’s create a subclass colorpoint with one more property color and one more method changecolor. Unfortunately we have to consider separately inheritance of value properties and inheritance of methods.
Regarding value properties it is possible to repeat creation of superclass properties in the subclass constructor. There are two reasons against this approach: first there is redundant code and what’s more important, any modification in the superclass must be repeated in all subclasses with obvious danger of inconsistency. The solution is a function used both by the superclass and the subclass:
Inheritance
outlined in the previous example can continue – colorpoint can be used as a
superclass etc. Note that in order to allow inheritance; constructors just call
functions that create the properties. Of course private methods can be
inherited in the same way as value properties.
Methods stored in prototypes can be inherited either by replacing the whole prototype object or by copying the methods. The first method can be used in our example in this way:
colorpoint.prototype = new point(0,0);
The first statement replaces the standard prototype by a point instance; the second statement creates the new method. There are two flaws – first the new prototype has also the two value properties (x and y). It is not a mistake. Assuming that the constructor creates properties with the same names, prototype read-only properties are not visible and the only problem is wasted memory. The second flaw is more serious. All prototypes have a property constructor that is a reference to the function object of the constructor function that has created this object. It can be very useful to check types of instances (like “is” in Simula). Obviously by replacing the standard prototype by another object as in the above example, the constructor property also changes. To get exactly what we want, methods have to be copied from superclass to subclass. The following function uses the fact, that objects in JavaScript can be treated as associative arrays and a special form of the “for” statement based on this fact:
function
inherit(from,to) {
for(var p in
from.prototype)
if (typeof
from.prototype[p] == "function")
to.prototype[p] = from.prototype[p]
};
inherit(point,colorpoint);
The first statement copies all prototype methods; the second statement creates the new method.
Polymorphism
Polymorphism is basically not compatible with strong typing. That’s why classical compiled OOLs introduce late binding through virtual methods that represents probably the most complicated part of OOP. Note that Java does not have virtual methods, but it means that all methods are in fact virtual. Programmer’s comfort is paid by time. Interpreted loosely typed JavaScript is polymorphic by nature. Moreover polymorphism is not limited to inheritance sequences. Consider the next two statements: p = x; p.m(); They will work for any object x that has a method m. JavaScript does not perform any type check, everything is the programmer’s responsibility. So the flexibility is paid by very limited security. That’s why JavaScript can not compete with classical OOLs in large software development projects.
Other techniques
Interpreted JavaScript enables techniques not conceivable in compiled strongly typed OOLs. Among others the following is possible:
Adding instance properties and methods can be a fast alternative to inheritance, especially in case of small number of instances. At any time it is possible to create new properties and methods:
origin = new
point(0,0);
p =
new point(ix,iy);
p.d = point.distance(origin,p); //New property of p
p.dupdate
= function() {
//New method of p
this.d = point.distance(origin,this)
};
Modification of instance properties and methods is also possible. It can be used for example as an alternative to status variables. Instead of testing a status, activate directly the method that has been updated accordingly. It is also possible to change a method into a property and vice versa, but then they have to be treated accordingly.
Partial inheritance is a technique not allowed in OOLs. Nevertheless there are situations when a simplified version of a certain class is required. This technique has been used in JSSim to create a discrete random distribution object as a simplified version of general random distribution object that has already been available. The point is inheriting only some methods (obviously they must be self-sufficient). The following example shows another version of the function inherit - actually the one available in JSSim and its use. The function first tests the number of actual parameters passed to it. If there are two parameters it copies all methods as in the above example. Otherwise it assumes that after the first two object parameters there is a list of strings – names of methods to be copied:
function
inherit(from,to) {
if
(arguments.length == 2) { // Inherit all
for(var
p in from.prototype)
if (typeof from.prototype[p] == "function")
to.prototype[p]
= from.prototype[p]
} else { // Inherit the listed
methods
for
(var i=2; i<arguments.length; i++)
to.prototype[arguments[i]] =
from.prototype[arguments[i]];
}
};
inherit(Distribution,DiscreteDistribution,
'fixtable','last','compareWithLastValue','showTable',
'accept','edit','insert','deleteit','cleartable',
'confirmtable','generate','save','load');
Only the 13 listed methods are
inherited.
Conclusion
JavaScript programmers can use all fundamental techniques of OOP together with new techniques offered by loose JavaScript typing.
![]()
3 JSSim Basic Ideas
JSSim is a collection of JavaScript declarations that together with appropriate HTML documents support user-friendly development of web hosted tools that contain simple and medium scale simulation models. Simulation models based on JSSim are incorporated into HTML documents. HTML code implements the link between the model and the user – it is used for inputs and outputs of the model and to control it. JavaScript code is made of two parts – JSSim JavaScript source file(s) and the user JavaScript code, preferably also in a separate file. All JSSim declarations are included in the file jssim.js, so a heading of the HTML document is supposed to contain the following script tag:
<SCRIPT LANGUAGE="JavaScript"
SRC="jssim.js"></SCRIPT>
JSSim also exist as a collection of separate source files, so in order to save loading time of the document it is possible to include only files with used declarations. User JavaScript code can be written either directly in a script tag as it is done in the demo examples, or preferably in a separate js file referenced by a script tag similar to the one above. There will also be short snippets of JavaSript code written directly in HTML tags – for example validation of input data. These snippets can be just calls to functions written either by the user or standard JSSim validation functions – see later.
Facilities found in languages and tools for programming discrete simulation models can be classified into the following main groups:
-
Time
control, synchronization and
communication of processes
-
Generation
of random numbers
-
Transparent
collection of statistical data and statistical analysis
-
Advanced
data structures
-
User-friendly
Input and Output
Next chapters will summarize the implementation of these facilities in JSSim together with specific functions given by the web-hosted nature of the models.
To select the time control of JSSim models we have considered only the
two commonly used approaches. While the process-oriented discrete
simulation represents the most advanced way of modeling the dynamics of complex
systems, the classical event-oriented approach is simpler and easier to
learn and to implement. That’s why it has been chosen for a JavaScript based
tool that is not intended for large simulation studies. Assuming that the
reader is familiar with the event-oriented principle, these are the basic
facts: During (re)loading of the document the engine
creates two global variables: the time
and the empty sequencing set (SQS – name borrowed from Simula). Events
are represented by event notices created by the user and stored in the
SQS. Each event notice has the
occurrence time of the event and any other user-defined
data. The engine assigns the time when the event is scheduled. From the user’s
point of view, the SQS is a list of event notices ordered by the time of
occurrence in increasing way. After activation, the engine repeatedly removes
the first event notice from SQS, updates the model time, and activates a user
routine that is given the reference to the event notice. Simulation ends by the
empty SQS or by any user supplied condition. These are the engine routines that
are called from the user’s part of the simulation model:
initialize_run() is a routine that clears the SQS (the previous experiment may have finished with nonempty SQS) and sets the model time to zero. It should be called at the beginning of the model initialization.
evnotice() is the event notice constructor. It returns an object with the time property that is used later by the engine and should not be accessed by the user. The user can add any other properties to distinguish between types of events and to store other model dependent data.
schedule(event,t) schedules the event whose notice is the first parameter at the time given by the second parameter. It is not possible to go back in time, so for t less than modeltime() the event is scheduled at modeltime().
modeltime() is the current time of the model. Scheduling an event e after a delay d is performed as follows:
schedule(e,modeltime()+d)
cancel(event) cancels a scheduled event. The function returns a Boolean value that reports whether canceling was successful – the function returns false if event has not been scheduled.
sim_run(stats,length,run,expers) starts the simulation experiment. This routine should be called after the model initialization that has to schedule at least the first event. The first two arguments control the progress reporting in the status bar. If stats is true, time progress will be reported, length is shown as the duration of the experiment. If stats is false, only the run number is shown. The last two arguments are the current run number and the total number of repetitions. The routine ends by reaching the empty SQS or by the user supplied terminating condition - the user’s routine finish_run().
simulation_run(stats,length) starts the simulation experiment. It is the old version of the above routine before repetitions were implemented. It is kept for compatibility of older models.
The above routines are
common to all simulation models. Model specific behavior is implemented by two
routines that have to be supplied together with the code (preferably
also a routine) that starts the simulation. These are the routines (together
with examples) that represent the user’s part of the simulation control:
finish_run() tests whether simulation should be terminated. It is called by the engine after updating the model time just before activating the next event. It can just test the time against the experiment duration or it can implement a more complicated terminating condition, like for example serving a given number of customers. The following is the function of a model where the experiment is finished by reaching its duration runlength:
function finish_run() {
return
(modeltime()>runlength)
};
eventroutine(event) is activated by the engine each time an event is to occur. The routine is given the reference to the event notice that has been removed from the SQS. The rest is the user's responsibility. Typically there will be some properties created by the user used to switch between various types of events. It might be a good idea to keep this routine short and simple and to write routines for various types of events similarly as they are written in event oriented simulation languages. The following is the function of a model with two types of events. Note that the event notices have two user-defined properties: eventtype and servnum (the server number):
function eventroutine(event) {
switch
(event.eventtype) {
case 1: next_arrival(); break;
case 2: end_of_service(event.servnum); break;
default:
alert("Wrong eventtype: " + event.eventtype)
}
};
The start of
simulation has also to be programmed. For example it can be a function
activated by pressing a button “Run”. This function is supposed to perform the
following activities exactly in this order:
- Initialization of the engine by initialize_run()
- Model specific initialization
- Starting simulation by simulation_run()
- Model specific experiment evaluation.
The following is an example of a function activated by pressing the button “Run” and its link to HTML for the single queue simulation model version #1.
<INPUT
TYPE="button" VALUE="Run" onClick="simulation()">
function simulation() { //
Simulatiom experiment
if
((arrival.disttype=="User") && !(arrival.confirmed)) {
alert("Can't
start simulation. Arrival intervals table
has not been
confirmed.");
return false;
};
if ((service.disttype=="User")
&& !(service.confirmed)) {
alert("Can't
start simulation. Service duration table
has not been
confirmed.");
return false;
};
initialization(); // Model global initialization
runnumber = 1;
while
(runnumber<=numofexp) { //
Repetitions loop
initialize_run(); // This prepares the engine
run_init(); // Run initialization
nextarrival(); // Scheduling first arrival
sim_run(showstatus,runlength,runnumber,numofexp);
// This starts the
simulation
lqe.update(queue.average());
// queue length statistics
wqe.update(wtime.average());
// queue time statistics
le.update(ssize.average()); // system size statistics
we.update(stime.average()); // system time statistics
runnumber++;
};
evaluation(); // Experiment evaluation
return true;
};
JSSim contains a rather complex class used to generate instances (objects) that represent random numbers. These can have either a theoretical distribution, but primarily they are supposed to contain tables used to generate values with a general (for example experimentally obtained) distribution. Methods are available for entering and editing such tables. Working with empirical tables is user-friendly; table entries can be modified, inserted and deleted. Table can be entered as a cdf (cumulative distribution function) or a pdf (probability distribution function). In both cases there is a re-calculation to the other type. During editing tables can be left temporarily inconsistent, but before use a table has to be checked and confirmed. Both values and cdf entries must form non-decreasing sequences. Sum of probabilities has to be 1; a confirmation method offers adjustment of the last entry if the sum is smaller. Associated HTML text contains a help that explains the basic ideas and the inversion method, so only basic knowledge of probability is assumed. Large tables can be saved and loaded (provided cookies are enabled in the browser). Figure 1 shows a table created by HTML used to enter parameters of a random variable. The controls are self-explaining. Figure 1 shows the situation just after confirmation of an empirical cdf table by pressing the button “Check & Confirm”. Inversion is used for generation that can be either discrete or interpolated. The technique of restricted inheritance (simplification) mentioned earlier was used do declare a simplified version of this class for generation of discrete random numbers with empirical distribution only. Its instances have been used for example to represent random movements of customers in queueing networks. Work with random numbers is very simple. Instances are first created by statements similar to the following one located typically in the head code that is interpreted during loading of the document:
var arrival = new Distribution("a1");
The method generaten(n) returns the random values generated by the random stream n. So during simulation statements similar to the next one are used:
var x = arrival.generaten(1);
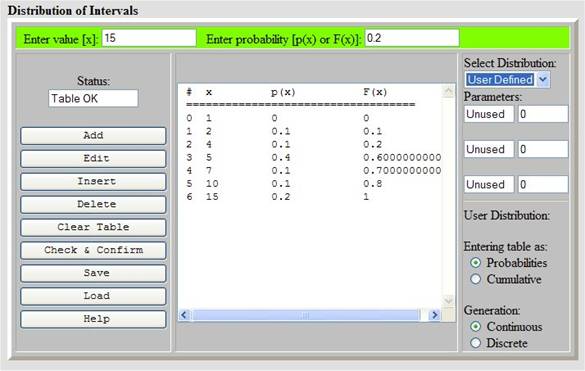
Figure 1: Entering parameters of a random variable
Initially JSSim used the standard JavaScript random generator Math.random(). Later a Linear Congruential Generator (LCG) has been implemented with constants known as MINSTD (Minimum Standard) that passed all usual tests. JSSim contains routines for initialization and use of any number of random streams, for details see the code. To keep compatibility, the random objects now contain two generation methods. One is using the standard generator Math.random(), the other one is using a JSSim random stream of a given number.
The following is the class summary of the random object that lists the constructor, the value properties that might be useful, and the methods. Next we shall keep this format. For more details see the JavaScript code and the examples.
Class
Distribution
Constructor
Distribution(name) .name = object and screen text name
Properties
status user table distribution status
confirmed whether user distribution has been
confirmed
disttype type of distribution
enterMode entering mode (pdf, cdf)
generMode generation mode (continuous,
discrete)
Methods
scrupdate() screen update
update(index) internal update
index = distribution
type
testpar1(tx) testing first distribution parameter
tx = tested value
(text)
testpar2(tx)
testing second distribution
parameter
tx = tested value
(text)
fixtable() conversion pdf – cdf
last() index of last table entry
compareWithLastValue(textElement) testing next table entry
textElement = the
text value
showTable() converting table to text form
accept(tx,tp) acceptind value,probability pair
tx = value
tp = probability (or
cdf value)
edit() editing a table entry
insert() inserting a table entry
deleteit() deleting a table entry
cleartable() erasing the table and data
confirmtable() checking the table
generate() generating
next random value by using the standard JavaScript generator Math.random()
generaten(n) generating
next random value by using the native JSSim LCG generator
n = number of random stream used
toString() converting all parameters to string
save(cn) saving to a cookie
cn = cookie name
load(cn)
loading from a cookie
cn = cookie name
fromString(cv) extracting parameters from a string
cv = string
Class
DiscreteDistribution
Constructor
DiscreteDistribution(name) name = object and screen text name
Properties
status user distribution status
confirmed whether user distribution has been
confirmed
disttype type of distribution
enterMode entering mode (pdf, cdf)
generMode generation mode (continuous,
discrete)
Methods
scrupdate() screen update
fixtable() conversion pdf – cdf
last() index of last table entry
compareWithLastValue(textElement) testing next table entry
textElement = the
text value
showTable() converting table to text form
accept(tx,tp) acceptind value,probability pair
tx = value
tp = probability (or
cdf value)
edit() editing a table entry
insert() inserting a table entry
deleteit() deleting a table entry
cleartable() erasing the table and data
confirmtable() checking the table
generate() generating
next random value by using the standard JavaScript generator Math.random()
generaten(n) generating
next random value by using the native JSSim LCG generator
n = number of random stream used
toString() converting all parameters to string
save(cn) saving to a cookie
cn = cookie name
load(cn)
loading from a cookie
cn = cookie name
fromString(cv) extracting parameters from a string
cv = string
To collect statistics of a
certain variable x automatically, it is necessary to update certain
figures (like for example its time integral) after each updating of x.
In other words all assignment statements that have x on the left side
must also activate a certain routine that updates what is necessary. Simulation
languages like Simscript do it automatically (Simscript calls this mechanism left monitoring), but
there is of course nothing like that in JavaScript. Transparent collection of statistical data and simple statistical
analysis are implemented by the classes Accumulator and Tally (Simscript terminology is used). The instances of these two classes
are basically real variables with transparent collection of statistics. The
consequence for the user is the difference in the form of the assignment
statement. The usual a = x has to be
replaced by a method call a.updateto(x). They differ in time treatment.
Tally ignores the
time; the statistics is based on the collection of the assigned values only.
Objects of the class Tally are thus used for figures whose statistics does not
depend on time integrals. As an example consider time spent in a queue. It is
calculated for each customer at the beginning of the service by subtracting the
time when the customer arrived to the queue from the current time. Each
calculation then updates the statistical object. The following has to be done:
1) Tally object is created, typically by the head code:
waitingtime
= new tally();
2) Before starting the experiment the Tally object has to be
initialized:
waitingtime.initiate();
3) For each customer it is
updated similarly as follows where cust
is the customer handle and sertimein is the arrival time:
waitingtime.update(modeltime()
- cust.sertimein);
4) During evaluation methods with results are used directly, for
example as follows:
document.netform.SR8.value
= waitingtime.average();
Accumulator statistics is based on time integrals. An example of its use is a queue length whose average value depends on time integral of the queue length. From user’s point of view use of Tally and Accumulator objects is almost identical.
Class
Tally
Constructor
tally()
Properties
max maximum value
min minimum value
sum sum of assigned values
sumSq sum of squares of assigned
values
updated number of updates
Methods
initiate() object initialization
scrupdate(dname) screen results update
dname = screen text
element name
winupdate(stitle,w) windows results update
stitle = title string
w = window object
update(newx) object update
newx = the new value
average() average
variance() variance
stdDev() standard deviation
Class
Accumulator
Constructor
accumulator(x) x = the initial value
Properties
value current value
max maximum value
min minimum value
sum time integral of value
sumSq time integral of squared value
initTime initialisation time
lastTime last update time
Methods
initiate(x) object initialization
x = the initial value
scrupdate(dname) screen results update
dname = screen text
element name
winupdate(stitle,w) windows results update
stitle = title string
w = window object
updateto(newx) object update
newx = the new value
updateby(delta) object update
delta = the increment
average() average
variance() variance
stdDev() standard deviation
To implement the sequencing set that is conceptually an ordered list of event notices the heap class has been implemented. Heap (not to be mixed with the dynamically allocated memory of some languages) is a perfectly balanced binary tree stored in an array with the following properties assuming ascending ordering of items by a certain key:
- The root with minimum key is at the position 1
- The two children (if any) of a node at the position i are at the positions 2i and 2i+1
- Both children have bigger (or equal) key than the parent.
Heap supports two basic operations adding an item and removing the first item. These operations have the performance of O(log2n) where n is the number of items in the heap. Heap could also be used as a priority queue, though there is another declaration for this purpose – see later. JSSim also contains classes that implement a linked list and a generic statistically monitored queue without any specific ordering. Using these two classes as superclasses, programmed multiple inheritance was used to define class for FIFO queues. Due to the superclasses used in multiple inheritance, the FIFO queues can have practically unlimited length and methods are available that return typical statistical results like average, standard deviation, and maximum of the queue length. Class for FIFO queues was then used as a superclass to declare LIFO and priority queues. These two classes share the methods with the FIFO superclass except the method enqueue that had to be modified. Methods that perform the basic operations have the same name. Loosly typed JavaScript is polymorphic, so the same code can be used to work with various types of queues. This is the inheritance tree of the 5 types of queues (and Heap):
JSSim data structures inheritance tree:
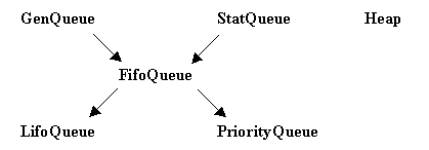
Description of the classes:
Class
Heap
Constructor
Heap(name) name = object name
Properties
hname object name
hsize actual length (number of items)
Methods
empty() whether a heap is empty
clear() erasing heap data from RAM
insert(x) inserting x to heap
x = item with x.key property
remove(x) removes x from heap
x = item to be removed
restoreheap(i) restores heap from position i down
i = starting index
getfirst() removes and returns the first item
Class
GenQueue (generic queue – linked list)
Constructor
GenQueue(name) name = object name
Properties
qname object name
first reference to first item
last reference to last item
qlength actual length (number of items)
Methods
empty() whether a heap is empty
geninit() queue (linking) initialization
Class
StatQueue (generic statistically monitored queue)
Constructor
StatQueue()
Properties
qlength actual length (number of items)
maxqlength maximum queue length
qlsum queue length integral
qlsumsq squared queue length integral
initTime initialization time
qlsumt queue length integral last update
Methods
statinit(tim) queue initialization
tim = initialization
time
scrupdate(dname) screen results update
dname = screen text
element name
winupdate(stitle,w) windows results update
stitle = title string
w = window object
accumulate() integrals update (to be done before
change)
average() average queue length
variance() queue length variance
stdDev() queue length standard deviation
Class
FifoQueue = subclass of GenQueue and StatQueue
Constructor
FifoQueue(name) name = object name
Properties
(inherited ones
from GenQueue and StatQueue)
Methods
(inherited ones
from GenQueue and StatQueue plus:)
initiate(tim) queue initialization
tim = initialization
time
enqueue(x) enqueue an item
x = item to be inserted (no type assumed)
removefirst() removed first item (null if empty)
Class
LifoQueue = subclass of FifoQueue
Constructor
LifoQueue(name) name = object name
Properties
(inherited ones
from FifoQueue)
Methods
(inherited ones
from FifoQueue) enqueue(x) modified
Class
PriorityQueue = subclass of FifoQueue
Constructor
PriorityQueue(name) name = object name
Properties
(inherited ones
from FifoQueue)
Methods
(inherited ones
from FifoQueue) enqueue(x) modified
This chapter summarizes routines that do not implement JSSim classes, but may be useful even for general use. For details see the JSSim code and/or JavaScript documentation.
General
Purpose Routines
listProperties(obj) displays all object properties in an alert
window (useful for debugging)
spaces(n) returns text made of n spaces
help(x) opens the help window, shows x in
it
x = HTML help document
help
window size and location parameters can be modified.
defaults: winhelpwidth = 600 winhelpheigth = 400
winhelphorpos
= 20 winhelpverpos = 50
Data
Validation
(x
= text to be tested, alert shown if error detected)
syntaxOK(x) syntax of a number
testIntValue(x) syntax of an integer number
testPosIntValue(x) syntax of a positive integer
testNonNegIntValue(x) syntax of a nonnegative integer
testExper(x) experiment duration (positive number)
testNonnegLE1Value(x) probability(non-negative
number not
greater than 1)
OOP - Inheritance
inherit(from,to[,methods]) programmed inheritance
from = superclass
prototype
to = subclass
prototype
methods = list of
methods (all by default)
Cookies
saveCookie(name,value,expire) saving a cookie
name = cookie name
value = cookie value
expire = expiration
date
writeCookie(name,value,ndays)
saving a cookie
name = cookie name
value = cookie value
ndays = expiration
after ndays days
readCookie(name) returns a cookie value or null
name = cookie name
cookietoString(name) returns a cookie value or a message
name = cookie name
9 Input/Output General
Guidelines
Validated input is easily implemented by JavaScript code associated
with text areas in the HTML document. JSSim contains various validation
routines to check for example that the user has entered a syntactically correct
non-negative number. In addition to validation it is also possible to update
model parameters accordingly. This can simplify model initialization when
simulation is started. The following HTML fragment together with the associated
page contents represents a validated input of a probability value. The routine
checks non-negativity and whether the value is not bigger than 1. Note that 0
is restored in case of wrong input.
Enter
probability [p or F]:
<INPUT
TYPE="text"
NAME="GIpx" SIZE=15
VALUE="0.0"
ONCHANGE="
if(!testNonnegLE1Value(GIpx.value))
{GIpx.value = 0}">
![]()
Model parameters can be updated directly when the user enters the
values or alternatively it is possible to link objects to HTML text fields and
to write methods that read the validated data before simulation starts. This
direct link has so far been utilized for outputs. The idea is as follows. The
link is done by common names. So assume that a queue instance has been created
by calling its constructor:
queue = new
FifoQueue("Q1");
The constructor creates and initializes the queue,
the name is stored to the property qname.
The instance has two output methods inherited from statistically monitored
queue. The first method is used to update the contents of the host HTML
document:
StatQueue.prototype.scrupdate = function(dname)
{
with (this) {
eval(dname + qname + "av.value = average()");
eval(dname + qname + "ma.value = maxqlength");
eval(dname + qname + "sd.value = stdDev()");
}};
Note that the method scrupdate() updates three text fields (typically in a table
with results) that would contain the average length, the maximum length, and
the standard deviation of the length of the queue. Assume that the method is
called as follows:
queue.scrupdate("document.form1.");
So for the average and with respect to the above example the procedure eval is given and evaluates the parameter:
document.form1.Q1av.value=average()
This updates the text field called Q1av on the screen. The following is the HTML fragment together with the
associated page contents:
<TH> Average </TH>
<TD><INPUT TYPE="text" NAME="Q1av"
SIZE=25></TD>
![]()
So far it is the user’s responsibility to keep the compatibility of
names. Here it is the name of the JavaScript object Q1 that is linked to the HTML text field called
Q1av. This can be achieved by using standard HTML
templates processed by the “Replace All” operation available in practically all
text editors. In this case a template displaying typical queue statistics would
be used. Another method winupdate() generates an HTML fragment that
displays four lines with results:
StatQueue.prototype.winupdate = function(stitle,w)
{
with (this) {
w.writeln(stitle + " length statistics:" + "<BR><UL>");
w.writeln("<LI> Average: " + average());
w.writeln("<LI> Maximum: " + maxqlength);
w.writeln("<LI> Std Dev: " + stdDev() +
"</UL>");
}};
The method winupdate() is used for generation of results
in textual format in a separate window. Assuming that there is an open window resw the method is
activated as follows:
var d =
resw.document; ...
queue.winupdate("Queue",d);
The generated output can then be copied and pasted into
other documents as it has been done here:
Queue length statistics:
- Average: 0.6672205803062008
- Maximum: 10
- Std Dev: 1.4089986068350546
This example just shows how to work with events. All should be clear from Figure 2. The following is the complete HTML code:
<HTML>
<HEAD>
<TITLE>JSSim Example
#1</TITLE>
<SCRIPT LANGUAGE="JavaScript"
SRC="jssim.js"></SCRIPT>
<SCRIPT LANGUAGE="JavaScript">
//****************** USER SIMULATION ROUTINES *******************
function
finish_run() { // Finish run ? (must be supplied)
return
(modeltime()>runlength);
};
//...............................................................
function
eventroutine(event) { // The event
routine
alert("Event of
type " + event.eventtype + " starts at time "+
modeltime() +
". SQS length = " + SQS.hsize);
switch
(event.eventtype) {// switching between types of events
case 1:
event1(); break;
case 2:
event2(); break;
case 3:
event3(); break;
case 4:
event4(); break;
default:
alert("Wrong
eventtype: " + event.eventtype);
};
alert("Event of
type " + event.eventtype +
" ends.
SQS length = " + SQS.hsize);
};
//======================
Event routines =========================
function
event1() {
var ev = new
evnotice(); // event 1 schedules events 2 and 3
ev.eventtype = 2;
schedule(ev,12);
notice = new
evnotice();
notice.eventtype = 3;
schedule(notice,13);
};
//...............................................................
function
event2() {
var ev = new
evnotice(); // event 2 schedules event
4
ev.eventtype = 4; // and may cancel event 3
schedule(ev,44);
if (confirm('Confirm
whether to cancel the Event 3')) {
cancel(notice);
};
};
//...............................................................
function
event3() {
};
//...............................................................
function
event4() {
};
//===================
Starting Routine ==========================
function
simulation() { // Simulatiom run
initialize_run(); // This prepares the engine
// System parameters (if any):
runlength =
document.forms[0].I1.value; // retrieve duration
// Preparation - at least one event has to
be scheduled:
var ev = new
evnotice();
ev.eventtype = 1;
schedule(ev,1);
simulation_run(document.forms[0].I2.checked,runlength);
alert("Evaluation
at time " + modeltime()); //
Evaluation
};
//======================
Head Code ==============================
// Global variables:
var
runlength = 0; // length of the
experiment
var
notice = null; // event notice
to cancel later
//===============================================================
</SCRIPT>
</HEAD>
<BODY
BGCOLOR="#000000" TEXT="#00ff00" LINK="#ffff00"
VLINK="#afaf00">
<FORM
NAME="tester">
<CENTER><H1>JSSim
- Example Simulation #1</H1></CENTER>
<HR>
<P ALIGN=JUSTIFY>
This document is a very
simple simulation experiment. Look at
the
source code of this document to see how the simulation experiment has been
programmed.
</P>
<HR>
<H3><B>Experiment
Control:</B></H3>
<INPUT
TYPE="button" VALUE=" Run "
onClick="simulation()">
Experiment Duration:
<INPUT
TYPE="text" NAME="I1" SIZE=5 VALUE="1000">
Show Status: <INPUT TYPE="checkbox"
NAME="I2" CHECKED>
<P><HR>
<H3><B>Short description:</B></H3>
<P ALIGN=JUSTIFY>
There is a text input to
enter the experiment duration and a check
box
to turn on/off the status bar reporting. Simulation is started by pressing the
button Run that activates the routine <B><I>simulation()</I></B>.
It initializes the model and schedules the Event1 at time 1. The Event1
schedules the Event2 and the Event3 at times 12 and 13 respectively. The Event2
schedules the Event4 at time 44 and possibly cancels the Event3. Starts and
ends of all events are reported together with SQS length.
Try short experiment duration
(for example 20).
<P><HR>
</FORM>
</BODY>
</HTML>

Figure 2: Example 1 screen
You can run the example 1 simulation now.
Example 2 models a single queue system with server failures. The simulated system is defined as follows:
- Exponential single arrivals from unlimited population, one class of customers.
- Unlimited capacity FIFO queue.
- One server with normally distributed service duration.
- Server breaks down with exponentially distributed intervals between failures.
- Uniformly distributed repair time.
- Item whose service is interrupted is after the repair served again.
The system is kept simple intentionally. Many assumptions can be easily relaxed. The required outputs are:
- Average and maximum waiting time.
- Average, minimum and maximum time spent in the system.
- Queue length statistics.
The user's part of the JavaScript code is included in the HTML document intentionally for the reader to read it easily during the browser session. Otherwise it might be better to create a separate js file with the user code to keep the HTML document short. The following is the complete HTML code:
<HTML>
<HEAD>
<TITLE>JSSim Example
#2</TITLE>
<SCRIPT LANGUAGE="JavaScript"
SRC="jssim.js"></SCRIPT>
<SCRIPT LANGUAGE="JavaScript">
//**************** USER SIMULATION ROUTINES *********************
function
finish_run() { // Whether to finish
run
return
(modeltime()>runlength);
};
//...............................................................
function
eventroutine(event) { // The event
routine
switch
(event.eventtype) { // switching
between event types
case 1:
arrival(); break;
case 2:
end_of_service();
break;
case 3:
breakdown(); break;
case 4:
end_of_repair();
break;
default:
alert("Wrong
eventtype: " + event.eventtype);
};
};
//======================
Event routines =========================
function
arrival() { // customer arrival
arrivals++;
var cust = new
customer(modeltime()); // creating the
customer
var ev = null;
if
((served==null)&&(serverOK)) { // can start service ?
served =
cust; // yes
waittime.update(0);
ev = new
evnotice(); // scheduling end of service
ev.eventtype = 2;
served.event = ev;
schedule(ev,modeltime()
+ normal(meanservice, serviceStd));
} else {
queue.enqueue(cust);
// no, wait
};
ev = new
evnotice(); // scheduling next arrival
ev.eventtype = 1;
schedule(ev,modeltime()
+ exponential(meaninterval));
};
//...............................................................
function
end_of_service() { // service ends
systemtime.update(modeltime()
- served.nettimein);
served = null;
if (!queue.empty())
{ // queue empty ?
served =
queue.removefirst(); // no - serve the 1st one
waittime.update(modeltime()
- served.nettimein);
var ev = new
evnotice(); // scheduling end of service
ev.eventtype = 2;
served.event = ev;
schedule(ev,modeltime()
+ normal(meanservice,serviceStd));
};
};
//...............................................................
function
breakdown() { // server failure
failures++;
serverOK = false;
if (served!=null)
{ // service on ?
cancel(served.event);
// yes - cancel it
};
var ev = new
evnotice(); // scheduling end of repair
ev.eventtype = 4;
schedule(ev,modeltime()
+ uniform(repairfrom,repairto));
};
//...............................................................
function
end_of_repair() { // server repaired
serverOK = true;
var ev = new
evnotice(); // scheduling next failure
ev.eventtype = 3;
schedule(ev,
modeltime() + exponential(meanbreakinterval));
if
((served==null)&&(!queue.empty())) { // new service ?
served =
queue.removefirst(); // yes - serve the 1st one
waittime.update(modeltime()
- served.nettimein);
};
if (served!=null)
{ // starting service ? (new or old)
ev = new
evnotice(); // scheduling end of service
ev.eventtype = 2;
served.event = ev;
schedule(ev,modeltime()
+ normal(meanservice,serviceStd));
};
};
//===============================================================
function
set_parameters() {// Retrieving model&control parameters
meaninterval =
parseFloat(doc.I11.value); // mean arr. Interval
meanservice =
parseFloat(doc.I21.value); // mean
service
serviceStd =
parseFloat(doc.I22.value); // service
std dev
// mean interval
between failures:
meanbreakinterval =
parseFloat(doc.I31.value);
repairfrom =
parseFloat(doc.I41.value); // minimum
repair
repairto =
parseFloat(doc.I42.value); // maximum
repair
runlength =
parseFloat(doc.CI1.value); // length of experiment
};
//...............................................................
function
evaluation() { // Experiment
evaluation
doc.R1.value = arrivals;
doc.R2.value = waittime.average();
doc.R3.value = waittime.max;
doc.R4.value = systemtime.average();
doc.R5.value = systemtime.min;
doc.R6.value = systemtime.max;
queue.scrupdate("document.forms[0].");
doc.R9.value = failures;
};
//===================
Starting Routine ==========================
function
simulation() { // Simulatiom
experiment
doc = document.forms[0];
initialize_run(); // This prepares the engine
set_parameters(); // Model & Control parameters
// Model & statistics initialization
queue.initiate(0);
served = null;
serverOK = true;
arrivals = 0;
failures = 0;
waittime.initiate();
systemtime.initiate();
// Preparation - at least one event has to
be scheduled:
var ev = new
evnotice(); // Scheduling 1st arrival
ev.eventtype = 1;
schedule(ev,exponential(meaninterval));
ev = new
evnotice(); // Scheduling 1st
failure
ev.eventtype = 3;
schedule(ev,exponential(meanbreakinterval));
// This starts the
simulation:
simulation_run(doc.CI2.checked,runlength);
evaluation(); // Experiment evaluation
};
//...............................................................
function
customer(tim) { // customer
constructor
this.nettimein = tim; // time of entering system
this.event = null; // end of service event notice
};
//========== Head Code
(creating global variables) ==============
// Model parameters
var
meaninterval = 0; // mean interval
between arrivals
var
meanservice = 0; // mean service
duration
var
serviceStd = 0; // service
standard deviation
var
meanbreakinterval = 0; // mean interval
between failures
var
repairfrom = 0; // minimum
repair time
var
repairto = 0; // maximum
repair time
// Model objects
var
queue = new FifoQueue('Q'); // the queue
var
served = null; // served customer
var
serverOK = true; // server status
// Control parameters
var
runlength = 0; // length of the
experiment
// Statistics
var
waittime = new tally(); // waiting time
var
systemtime = new tally();// system time
var arrivals
= 0; // # of arrivals
var
failures = 0; // # of failures
// Auxiliary
var
doc = null; // to access document
objects
//===============================================================
</SCRIPT>
</HEAD>
<BODY BGCOLOR="#000000"
TEXT="#00ff00" LINK="#ffff00"
VLINK="#afaf00">
<FORM
NAME="tester">
<CENTER><H1>JSSim
- Example Simulation #2</H1></CENTER>
<HR>
<P ALIGN=JUSTIFY>
This example is a simple
simulation experiment. The simulated
system is
a queueing system defined as follows:<BR>
<UL>
<LI>Exponential
arrival from unlimited population, one class
of
customers.</LI>
<LI>Unlimited FIFO
queue.</LI>
<LI>One server with
normally distributed service duration.</LI>
<LI>Server breaks
down with exponentially distributed intervals
between
failures.</LI>
<LI>Uniformly
distributed repair time.</LI>
<LI>Item whose
service is interrupted is after the repair served
again.</LI>
</UL>
The system is kept simple
intentionally. Many assumptions can be easily relaxed. The required outputs
are:
<UL>
<LI>Average and
maximum waiting time.</LI>
<LI>Average, minimum
and maximum time spent in the system.</LI>
<LI>Queue length
statistics.</LI>
</UL>
Look at the source code of
this document to see how the simulation
experiment
has been programmed. The user's part of the JavaScript
code
is included in this document intentionally for you to read it easily. Otherwise
it might be better to create a separate .js file
with
user code to keep the HTML document short.</P>
<HR>
<H3><B>Model Parameters:</B></H3>
(All times in minutes)
<TABLE BORDER>
<TR>
<TD>Exponential
intervals between arrivals</TD>
<TD>Mean: <INPUT TYPE="text"
NAME="I11" SIZE=5 VALUE="10"></TD>
<TD></TD>
</TR>
<TR>
<TD>
<TD>Mean: <INPUT TYPE="text"
NAME="I21" SIZE=5 VALUE="4"></TD>
<TD>Std: <INPUT TYPE="text"
NAME="I22" SIZE=5 VALUE="0.2"></TD>
</TR>
<TR>
<TD>Exponential
interval between failures</TD>
<TD>Mean: <INPUT TYPE="text"
NAME="I31" SIZE=5 VALUE="20"></TD>
<TD></TD>
</TR>
<TR>
<TD>Uniform repair
time</TD>
<TD>From: <INPUT TYPE="text"
NAME="I41" SIZE=5 VALUE="1"></TD>
<TD>To: <INPUT TYPE="text"
NAME="I42" SIZE=5 VALUE="10"></TD>
</TR>
</TABLE>
<P><HR>
<H3><B>Simulation
Control:</B></H3>
Experiment Duration:
<INPUT
TYPE="text" NAME="CI1" SIZE=5 VALUE="1000">
Show Status:
<INPUT
TYPE="checkbox" NAME="CI2" CHECKED value="ON">
<INPUT
TYPE="button" VALUE=" Run "
onClick="simulation()">
<P><HR>
<H3><B>Results:</B></H3>
<TABLE BORDER>
<TR>
<TD> Number of
arrivals </TD>
<TD> <INPUT
TYPE="text" NAME="R1" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Total
number of arrivals to
the
system.')"></TD>
</TR>
<TR>
<TD> Average waiting
time </TD>
<TD> <INPUT
TYPE="text" NAME="R2" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Average
time spent in the queue till first
start of
service.')"></TD>
</TR>
<TR>
<TD> Maximum waiting
time </TD>
<TD> <INPUT
TYPE="text" NAME="R3" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Maximum
time spent in the queue till first
start of
service.')"></TD>
</TR>
<TR>
<TD> Average time in
system </TD>
<TD> <INPUT
TYPE="text" NAME="R4" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Average
time spent in the system.')"></TD>
</TR>
<TR>
<TD> Minimum time in
system </TD>
<TD> <INPUT
TYPE="text" NAME="R5" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Minimum
time spent in the system. Note
that
minimum waiting time is zero.')"></TD>
</TR>
<TR>
<TD> Maximum time in
system </TD>
<TD> <INPUT
TYPE="text" NAME="R6" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Maximum
time spent in the system.')"></TD>
</TR>
<TR>
<TD> Average queue
length </TD>
<TD> <INPUT
TYPE="text" NAME="Qav" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Average
queue length including time when
it
was empty.')"></TD>
</TR>
<TR>
<TD> Maximum queue
length </TD>
<TD> <INPUT
TYPE="text" NAME="Qma" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Maximum
reached length of the queue.')"></TD>
</TR>
<TR>
<TD> Queue length std dev </TD>
<TD> <INPUT
TYPE="text" NAME="Qsd" SIZE=25> </TD>
<TD ALIGN="CENTER">
<INPUT TYPE="button" VALUE="Note"
onClick="alert('Standard
deviation of the queue
length.')"></TD>
</TR>
<TR>
<TD> Number of
failures </TD>
<TD> <INPUT
TYPE="text" NAME="R9" SIZE=25> </TD>
<TD
ALIGN="CENTER"> <INPUT TYPE="button"
VALUE="Note"
onClick="alert('Number
of server failures.')"></TD>
</TR>
</TABLE>
<P><HR>
</FORM>
</BODY>
</HTML>
Figures 3 and 4 show parts of the screen of the example 2. You can run the example 2 simulation now.
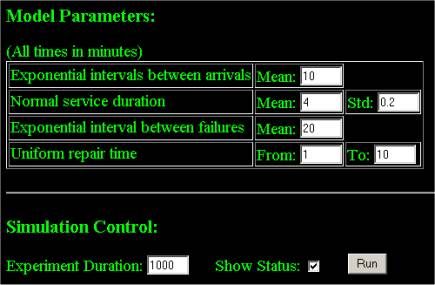
Figure 3: Example 2 screen – model parameters and controls
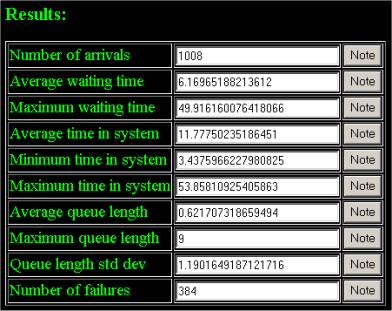
Figure 4: Example 2 screen – typical results (experiment duration 10000 min)
Further development of JSSim will be oriented to these areas:
- Implementation of all common theoretical random distributions
- Enhanced statistics (histograms)
- New classes supporting typical application areas
- HTML code snippets linked to output methods of standard model objects
- Support of repetitive experiments
- Support of debugging
- More examples
For new updates check the JSSim home page:
http://staff.um.edu.mt/jskl1/simweb/jssim/
[ Home | Simulation
| On-line Simulation | PetriSim
| Turbo Pascal | Simula
]
[ University Home
| Department of Statistics & OR ]